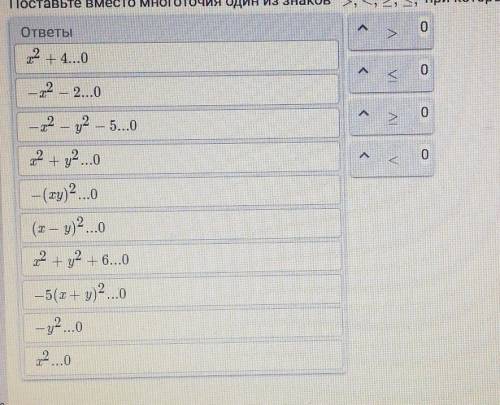
поставьте вместо многоточие один из знаков при котором получившееся неравенства будет верным при любых значениях x и y
Другие вопросы по теме Алгебра
Популярные вопросы
- Найдите решение систем уравнений или докажите,что системы не имеют решений...
2 - Помагите помагите 4. Прочитайте высказывания. Как вы их понимаете? Спишите...
1 - 2. Напишите структурную формулу аминокислоты, которая содержит 3 атома...
3 - Бжб казак тылы 7 сынып 4 токсан жауаптары...
2 - 1. Если соединим проводом тела, заряженные зарядом противоположных знаков,...
3 - Написать про любой город,страну (7-8 предложений...
2 - Сочинение можно ли назвать Андрея Соколова героем? 1) кто такой герой?...
1 - Почему в Италии и в Испании в 15-16 вв.работали так много скульпторов...
3 - Поезд за два дня проехал 1350 км . в первый день он был в пути 6ч а...
2 - В Vl -Vlll севернее г. полоцка проживали ...
3
В данном случае, нам дано неравенство -x - y < 0, где многоточие обозначает пропущенный знак.
Чтобы найти подходящий знак, рассмотрим возможные варианты.
1) "<" (меньше): Если мы используем знак "<", получим -x - y < 0. Это означает, что сумма -x и -y должна быть меньше нуля. Применяем свойство сложения противоположных чисел: -x + (-y) < 0. Затем, находим сумму: -(x + y) < 0. Здесь мы видим, что сумма (x + y) должна быть положительной, чтобы неравенство было верным. Однако, это не выполняется для всех значений x и y. Например, если x = 1 и y = -1, то -x - y = -1 - (-1) = 0, что не меньше нуля. Значит, вариант с знаком "<" не подходит.
2) ">" (больше): Если мы используем знак ">", получим -x - y > 0. Это означает, что сумма -x и -y должна быть больше нуля. Применяем свойство сложения противоположных чисел: -x + (-y) > 0. Затем, находим сумму: -(x + y) > 0. Здесь мы видим, что сумма (x + y) должна быть отрицательной, чтобы неравенство было верным. Когда сумма отрицательна, -x - y, как отрицательное число, будет больше нуля. Таким образом, вариант с знаком ">" подходит к заданному условию неравенства.
Итак, ответом на данный вопрос будет знак ">".
Таким образом, неравенство будет верным для любых значений x и y, когда используется знак ">" вместо многоточия.