1. Алгебра
  2. Последовательность задана

Последовательность задана рекуррентно: х(1)=1; х(n+1)=3х(n)+1. Задать эту последовательность формулой n-ого члена. Мне без разницы какими методами это будет решено, главно чтобы все было понятно из решения

WoudBack1 WoudBack1    2   01.06.2021 18:45    2

Ответы
5v09 5v09  01.06.2021 18:50

x_1=1;\ x_{n+1}=3x_n+1

Представим второе условие в виде:

x_{n+1}+k=3(x_n+k)

Определим k:

x_{n+1}+k=3x_n+3k

x_{n+1}=3x_n+2k

Сравнивая полученное соотношение с заданным, имеем:

3x_n+2k=3x_n+1

2k=1

k=\dfrac{1}{2}

Тогда, наше представление имеет вид:

x_{n+1}+\dfrac{1}{2} =3\left(x_n+\dfrac{1}{2}\right)

Проследим закономерность:

x_2+\dfrac{1}{2} =3\left(x_1+\dfrac{1}{2}\right)

x_3+\dfrac{1}{2} =3\left(x_2+\dfrac{1}{2}\right)=3^2\left(x_1+\dfrac{1}{2}\right)

x_4+\dfrac{1}{2} =3\left(x_3+\dfrac{1}{2}\right)=3^3\left(x_1+\dfrac{1}{2}\right)

...

x_n+\dfrac{1}{2} =3^{n-1}\left(x_1+\dfrac{1}{2}\right)

Подставим значение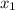 x_1:

x_n+\dfrac{1}{2} =3^{n-1}\cdot\left(1+\dfrac{1}{2}\right)

x_n+\dfrac{1}{2} =3^{n-1}\cdot\dfrac{3}{2}

x_n+\dfrac{1}{2} =\dfrac{3^n}{2}

Тогда формула n-ого члена:

\boxed{x_n=\dfrac{3^n-1}{2}}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
huxgehd huxgehd  05.06.2019 00:50
Решите неравенство методом интервала 1) 8x-9=2x^2+5x...
blowwwwwwww blowwwwwwww  05.06.2019 00:50
Люди! моя училка убьёт меня если решение не будет 1) (1+tgα/1+ctgα)+tgα 2) 1+cos5xsin4x=cos4xsin5x 3) sin(3 +x) /2 4) решите жизненно важно!...
adekvat3 adekvat3  05.06.2019 00:50
Составьте квадратное уравнение с целым коэффициентами, корни которого равны 3) -0,2 и -10 5) 0 и 6...
vishnya39 vishnya39  05.06.2019 00:50
Найти углы пятикутник если их градусная меры видносятся как 3: 2: 4: 4: 5...
Франц11 Франц11  03.07.2019 08:10
Решить систему уравнений ( x-y) (x^2-y^2)=45 x+y=5...
Olgadaleewa Olgadaleewa  03.07.2019 08:10
Представьте произведение в виде степени: 81с во 2 степени...
слава499 слава499  03.07.2019 08:10
Запишите в виде вырожения: 1)произведение суммы m и n на 10 второе2) сумму произведения m и n с числом 6: третье3) разность частного x и y и числа 12: четвертое4) частное...
eeeevaa eeeevaa  03.07.2019 08:10
Определите координаты центра и радиус окружности! 1)x^2+y^2+3x-4y=0 ответ (-1,5; 2) r=2,5 2)x^2+y^2-x-y-3=0 а.объясните откуда 2,5 б.решите второй с объяснениями. это : (!...
mirann2hsjb mirann2hsjb  03.07.2019 08:10
Приняв а=-3; b=4, c=7, на пишите уравнения вида ax+by+c=0...
333403 333403  11.07.2019 01:20
Записать в виде одночлена стандартного вида: 5a² * 6ab ³ b....

Популярные вопросы