Последовательность (cn) задана условиями: с1 = 2 и сn = cn-1 +2 при n> 1. найдите с6 ребзя

Ответы

Ilona9595 30.09.2020 17:59

$\tt \displaystyle C_{6}=12$

Объяснение:

Дана последовательность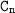 $\tt \displaystyle C_{n}$ :

$\tt \displaystyle C_{1}=2, \\\ C_{n}=C_{n-1}+2, \; n1.$

Так как

$\tt \displaystyle C_{n}-C_{n-1}=2, \; n1,$

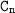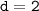то последовательность $\tt \displaystyle C_{n}$ является арифметической прогрессией и разность арифметической прогрессии равна: $\tt \displaystyle d=2$ .

Тогда по общей формулой арифметической прогрессии

$\tt \displaystyle C_{n}=C_{1}+(n-1) \cdot d, \; n1$

находим 6-член арифметической прогрессии:

$\tt \displaystyle C_{6}=2+(6-1) \cdot 2 =2+5 \cdot 2 = 2+10=12.$

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра

EmilN304 22.02.2020 20:11

У уравнение : -(x-5) +1 Вместо( ) - (в квадрате) ,...

masynchic 22.02.2020 20:15

В бригаде 20 рабочих, среди которых 5 штукатуров. Сколькими можно составить группу из 4 рабочих, в которой хотя бы один штукатур?...

EgorKornev665 22.02.2020 20:17

Задание на фото Решить не могу,не помню как ( 9 класс.Готовлюсь к экзаменам,это пробник)Подскажите как тема называется про упрощения выражений(?) как найти в Интернете...

Deverly1 22.02.2020 20:29

Известно, что в кошельке лежало n монет, каждая из которых могла иметь достоинство 2, 5 или 10 рублей. Лена сделала все свои покупки, расплатившись за каждую покупку отдельно...

Molly11111 06.12.2021 11:34

2. При каких значеннях и график функц уах проходит через точку А(3;9)...

pilipenkorita3 06.12.2021 11:33

Даны линейная функция y = -2х +3 Задайте формулой линейную функцию, график которой: а) параллелен графику данной функции; б) пересекает график данной функции; в) параллелен...

Лина14881 06.12.2021 11:33

решить графически систему уравнений...

віка812 06.12.2021 11:32

(4а нужно упростить и решить...

didlok 06.12.2021 11:32

перейдите на мой профиль решите хотяб сначала первый! Алгебра...

Дмитрий111111112222 06.12.2021 11:31

3.Найдите область определения функции, заданной формулой: 2x2x-3...

Последовательность (cn) задана условиями: с1 = 2 и сn = cn-1 +2 при n> 1. найдите с6 ребзя

Популярные вопросы