Порівняйте значення тригонометричних функцій 1) sin() і sin()
2) cos() і cos()

Ответы

emashewamarina 04.08.2022 10:18

1) $- \sin \displaystyle\frac{{7\pi }}{{30}} - \sin \displaystyle\frac{{9\pi }}{{30}};$

2) $\cos \displaystyle\frac{{10\pi }}{7} \cos \displaystyle\frac{{11\pi }}{9}$

Объяснение:

1) $\sin \left( { - \displaystyle\frac{{7\pi }}{{30}}} \right) = - \sin \displaystyle\frac{{7\pi }}{{30}};$

$\sin \left( { - \displaystyle\frac{{3\pi }}{{10}}} \right) = - \sin \displaystyle\frac{{9\pi }}{{30}}.$

Оба аргумента $\displaystyle\frac{{7\pi }}{{30}}$ и $\displaystyle\frac{{9\pi }}{{30}}$ принадлежат промежутку от до $\displaystyle\frac{\pi }{2}.$ В этом промежутке функция $y = \sin x$ возрастает. Это значит, что чем больше значение аргумента, тем больше значение функции. Отсюда

$\sin \displaystyle\frac{{7\pi }}{{30}} < \sin \displaystyle\frac{{9\pi }}{{30}},$ тогда $- \sin \displaystyle\frac{{7\pi }}{{30}} - \sin \displaystyle\frac{{9\pi }}{{30}}.$

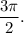2) Оба аргумента $\displaystyle\frac{{10\pi }}{7}$ и $\displaystyle\frac{{11\pi }}{9}$ принадлежат промежутку от $\pi$ до $\displaystyle\frac{{3\pi }}{2}.$ В этом промежутке функция 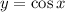$y = \cos x$ возрастает. Это означает, что чем больше значение аргумента, тем больше значение функции. Отсюда

$\cos \displaystyle\frac{{10\pi }}{7} = \cos \displaystyle\frac{{90\pi }}{{63}} \cos \displaystyle\frac{{77\pi }}{{63}} = \cos \displaystyle\frac{{11\pi }}{9}.$