Понять, как решаются такие уравнения: 1)cos 2x = 1; 2) cos t/3 = -1; 3) cos (4-2t) = 0; если можно, то подробно)

Question

Алгебра: Понять, как решаются такие уравнения: 1)cos 2x = 1; 2) cos t/3 = -1; 3) cos (4-2t) = 0; если можно, то подробно)​

вика3878 · Answer

1) cos2x=1

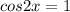
Находим все точки на окружности, у которых косинус = 1

Это право единичной окружности. Значение повторяется каждый круг. Значит все точки задаются выражением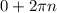 $0+2\pi n$

$2x=2\pi n \\ x=\pi n$

n везде целое

2) Аналогично. Ищем точки у которых косинус = -1

Это лево окружности

$\dfrac{t}{3}=\pi+2\pi n\\t=3\pi +6\pi n$ n всё ещё целое (но это уже не n из 1 примера, а очевидно другое)

3) cos чего-то равен 0. Значит это что-то =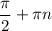 $\dfrac{\pi }{2}+\pi n$

$4-2t=\dfrac{\pi }{2}+\pi n\\ \\ 2t=4-\dfrac{\pi }{2}+\pi n\\ \\ t=2-\dfrac{\pi }{4}+\dfrac{\pi n}{2}$

n целое

Понять, как решаются такие уравнения: 1)cos 2x = 1; 2) cos t/3 = -1; 3) cos (4-2t) = 0; если можно, то подробно)​