понять как решается выражение
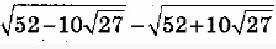
Другие вопросы по теме Алгебра
Популярные вопросы
- Климко йшов до міста ……. ? Скільки грошей взяв у Климка дядько(щвець) за взуття?...
2 - пожолуста нужна правильный ответ Казах; 1) a=4 м, b=3 м, с = 12 м; 2) а=1...
2 - Составьте кроссворд со словами: алгоритм, программа, язык, транслятор, компилятор,...
3 - Эссэ. Тема-снежная королева...
1 - опишите реку Нил по этому плану...
1 - Прочитай предложения, отметь те, в которых нет однородных ЧП. Знаки препинания...
3 - 10. Яке твердження є правильним? У роки боротьби за збереження державної незалежності...
2 - По данным схемам составьте предложения на тему «Зимний лес» [O, O]. [O и O]....
3 - Как влияет ритм на развитие усталости....
2 - 2. Check your vocabulary: gap fill Write the best word to complete the sentence....
2
В решении.
Объяснение:
√52 - 10√27 - √52 - 10√27;
1) Нужно разложить первое подкоренное выражение на квадрат разности.
10√27 = 2 * 5 * √27 (удвоенное произведение первого числа на второе).
Значит, первое число = 5, второе √27.
Преобразованное выражение под корнем:
√25 - 10√27 + 27 = √(5 - √27)² = |5 - √27| = √27 - 5.
Квадрат первого числа - удвоенное произведение первого числа на второе + квадрат второго числа.
Так как √27 больше 5, то |5 - √27| = -(5 - √27) = √27 - 5.
2) Разложить второе подкоренное выражение на квадрат суммы:
10√27 = 2 * 5 * √27 (удвоенное произведение первого числа на второе).
Значит, первое число = 5, второе √27.
Преобразованное выражение под корнем:
√25 + 10√27 + 27 = √(5 + √27)² = |5 + √27| = 5 + √27.
Квадрат первого числа + удвоенное произведение первого числа на второе + квадрат второго числа.
Так как сумма в модуле положительная, то |5 + √27| = 5 + √27.
3) Вычитание:
√27 - 5 - (5 + √27) = √27 - 5 - 5 - √27 = -10. ответ примера.