Помгите не знаю как решить
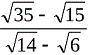
Другие вопросы по теме Алгебра
Популярные вопросы
- Скласти два речення зі словом холодний з прямим і переносним...
3 - Стих ночная страница найти в стихотворение словарные слова...
2 - Поставь іменники у формі множини.a head-heads,a shoulder? a knee? a toe? a...
3 - Земля,вращаясь вокруг солнца,за сутки проходит 2575000 км.сколько киллометров...
2 - Сделать предложения отрицательными и вопросительными . 1)at this time yesterday...
3 - Как связаны между собой градусные меры двух углов если а) эти углы равны б)...
3 - Написать изложение про костю и собаку боксера...
1 - Діалог на тему настрій перед новим роком...
1 - 2/3 денег афаг составляют 1/2 часть денег лалы сколько денег у афаг если вместе...
3 - Найдите площадь прямоугольника, если его периметр равен 244см,а ширина равна58см...
2
В решении.
Объяснение:
(√35 - √15)/(√14 - √6);
Чтобы избавиться от иррациональности в знаменателе, в данном случае нужно умножить дробь (числитель и знаменатель) на (√14+√6).
(√35 - √15)/(√14 - √6) * (√14 + √6)*(√14 + √6);
Тогда в знаменателе получится развёрнутая разность квадратов, которую нужно свернуть:
(√14 - √6)*(√14 + √6) = (√14)² - (√6)² = 14 - 6 = 8 (знаменатель).
Числитель:
(√35 - √15) * (√14 + √6) =
= (√7*5 - √3*5) * (√14 + √6) =
вынести общий множитель √5 за скобки для упрощения:
=√5 *(√7 - √3) * (√14 + √6) =
=√5 * (√7*√14 + √7*√6 - √3*√14 - √18) =
=√5 * (√98 + √42 - √42 - √18) =
=√5 * (√49*2 - √9*2) =
=√5 * (7√2 - 3√2) =
=√5 * 4√2 =
=4√10;
Новая дробь:
4√10/8 = √10/2 (ответ).
Можно дальше преобразовать ответ:
√10/2 = √10/4 = √5/2, всё под корнем.