1. Алгебра
  2. Пользуясь определением,найдите

Пользуясь определением,найдите производную функции f в точке x0 а)f(x)=x^2+1 x0=-2 б)f(x)=2/x x0=3 в)f(x)=2x-1 x0=-4 г)f(x)=x^3 x0=2 3.продифференцируйте функцию а)f(x)=(x+2)*sinx б)f(x)=4/(9+7x)^5 в)f(x)=x^3-2/x+cos3x г)f(x)=x^2/x+3

Tusya007 Tusya007    1   24.06.2019 10:20    3

Ответы
liloanimatronic liloanimatronic  02.10.2020 10:12

решение представлено на фото

Объяснение:


Пользуясь определением,найдите производную функции f в точке x0 а)f(x)=x^2+1 x0=-2 б)f(x)=2/x x0=3 в
Пользуясь определением,найдите производную функции f в точке x0 а)f(x)=x^2+1 x0=-2 б)f(x)=2/x x0=3 в
ПОКАЗАТЬ ОТВЕТЫ
привет8917 привет8917  02.10.2020 10:12

Определение производной функции через предел.

\displaystyle f'(x_0)= \lim_{x \to x_0}\dfrac{зf(x)}{зx}=\lim_{зx \to0}\dfrac{f(x_0+зx)-f(x_0)}{зx}=\lim_{x \to x_0}\dfrac{f(x)-f(x_0)}{x-x_0}

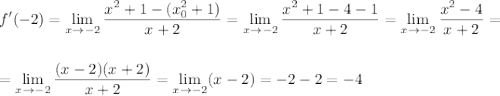
a) \displaystyle f'(-2)=\lim_{x \to -2}\dfrac{x^2+1-(x^2_0+1)}{x+2}=\lim_{x \to -2}\dfrac{x^2+1-4-1}{x+2}=\lim_{x \to -2}\dfrac{x^2-4}{x+2}=\\ \\ \\ =\lim_{x \to -2}\dfrac{(x-2)(x+2)}{x+2}=\lim_{x \to -2}(x-2)=-2-2=-4

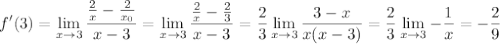
б) \displaystyle f'(3)=\lim_{x \to 3}\dfrac{\frac{2}{x}-\frac{2}{x_0}}{x-3}=\lim_{x \to 3}\frac{\frac{2}{x}-\frac{2}{3}}{x-3}=\frac{2}{3}\lim_{x \to 3}\frac{3-x}{x(x-3)}=\frac{2}{3}\lim_{x \to 3}-\frac{1}{x}=-\frac{2}{9}

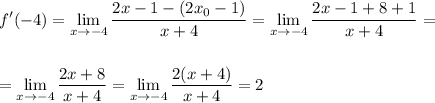
в) \displaystyle f'(-4)=\lim_{x \to -4}\frac{2x-1-(2x_0-1)}{x+4}=\lim_{x \to -4}\frac{2x-1+8+1}{x+4}=\\ \\ \\ =\lim_{x \to -4}\frac{2x+8}{x+4}=\lim_{x \to -4}\frac{2(x+4)}{x+4}=2

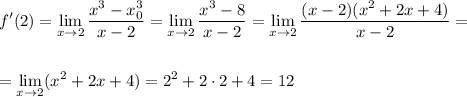
г) \displaystyle f'(2)=\lim_{x \to 2}\frac{x^3-x_0^3}{x-2}=\lim_{x \to 2}\frac{x^3-8}{x-2}=\lim_{x \to 2}\frac{(x-2)(x^2+2x+4)}{x-2}=\\ \\ \\ =\lim_{x \to 2}(x^2+2x+4)=2^2+2\cdot 2+4=12

3.

а) Продифференцируем функцию по формуле производной произведения: (uv)' = u' v + u v'

f'(x)=(x+2)'\sin x+(x+2)(\sin x)'=\sin x+(x+2)\cos x

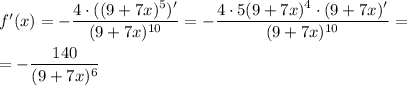
б) f'(x)=-\dfrac{4\cdot ((9+7x)^5)'}{(9+7x)^{10}}=-\dfrac{4\cdot 5(9+7x)^4\cdot (9+7x)'}{(9+7x)^{10}}=\\ \\ =-\dfrac{140}{(9+7x)^{6}}

в) Аналогично по формуле производной частного

f'(x)=\dfrac{(x^3-2)'(x+\cos 3x)-(x^3-2)(x+\cos 3x)'}{(x+\cos 3x)^2}=\\ \\\\ =\dfrac{3x^2(x+\cos 3x)-(x^3-2)(1-3\sin 3x)}{(x+\cos 3x)^2}

г) По формуле производной частного:

f'(x)=\dfrac{(x^2)'\cdot (x+3)-x^2\cdot (x+3)'}{(x+3)^2}=\dfrac{2x(x+3)-x^2}{(x+3)^2}=\dfrac{x^2+6x}{(x+3)^2}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
tanyaxxx15 tanyaxxx15  09.09.2020 01:53
Частка від ділення суми чисел 4/9 і -5/6 на число -14/24 ​...
sofija97 sofija97  09.09.2020 01:53
Укажите степень уравнения: 1) y2+xy-x5=0 2) y2+x2y2-x2=0 3) y2+3=(y-2)2...
danilgrekov20 danilgrekov20  10.09.2020 02:19
1) 6³ 2) 1, 4³ 3) (-8)⁴ 4) (-0,2)⁵ 5)(-2/3)⁴ Очень очень-очень-очень...
тагієва тагієва  10.09.2020 02:19
(2/7×7/5+1/5):5/3 с решением...
ppaulineppauline ppaulineppauline  26.09.2019 04:50
Решите уровнение: 2x^2+x+1/x^2+1=0...
nsalexandrovna nsalexandrovna  26.09.2019 04:50
Sos sos постройте график функции y=x² с графика определите,при каких значениях x значение у=4 с фотографией что-бы было все понятно.заранее ★...
Zaharza1 Zaharza1  26.09.2019 04:50
Автомобиль проехал половину пути со скоростью v1-60 км / ч . половину оставшегося времени движения он ехал со скоростью v3 -- 15 км / ч , а последний участок пути - со...
Катядонецк Катядонецк  26.09.2019 04:50
Решите систему уравнений методом сложения 3x-2y=6, 12x-8y=20...
AnnaVlasova09 AnnaVlasova09  26.09.2019 04:50
Является ли решением неравенства 2b+5 6b−17 значение b, равное 4,5? после решения неравенства получим, b __ __ значение b, равное 4,5 (является; не является) решением...
ladygum78 ladygum78  21.08.2019 17:40
Длины катетов прямоугольного треугольника равны 6 см и 8 см .вычеслите высоту проведеную к гепотенузе ....

Популярные вопросы