Положительное целое число a имеет два различных простых множителя p и q (p целое число b больше а и частное а
2
/ b является целым числом. сколько возможных значений
б есть?

Тогда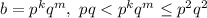

Для определённости возьмём p > q.

Найдём все возможные пары k и m, удовлетворяющие этому условию: (1; 2), (2; 1), (2; 2). Может ли быть такое, что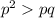 ? Да, если поделить на p, получим p > q, что верно. Значит, подходит ещё пара (2; 0).

ответ: 4