1. Алгебра
  2. полное решение со всеми пояснениями

полное решение со всеми пояснениями действий решений показательного уравнения: 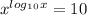x^{log_1_0x} =10

Karjal Karjal    1   30.08.2020 00:47    0

Ответы
IrynaShchutska IrynaShchutska  15.10.2020 16:27

\star \ \ log_{10}x=lgx\ \ \star \\\\\\1)\ \ x^{lgx}=10\ \,\ \ ODZ:\ x0\\\\lg(x^{lgx})=lg10\ \ ,\ \ \ lgx\cdot lgx=lg10\ \ ,\ \ lg^2x=1\ \ ,\ \ lgx=\pm 1\\\\a)\ \ lgx=-1\ \ ,\ \ x=10^{-1}\ \ ,\ \ x=0,1\\\\b)\ \ lgx=1\ \ ,\ \ x=10^1\ \ ,\ \ x=10\\\\Otvet:\ \ x=0,1\ ,\ x=10\ .

2)\ \ x^{4lgx}=10\ \ ,\ \ ODZ:\ x0\ ,\\\\4lgx\cdot lgx=lg10\ \ ,\ \ lg^2x=\dfrac{1}{4}\ \ ,\ \ lgx=\pm \dfrac{1}{2}\\\\a)\ \ lgx=-\dfrac{1}{2}\ \,\ \ x=10^{-1/2}\ \ ,\ \ x=\dfrac{1}{\sqrt{10}}=\dfrac{\sqrt{10}}{10}\\\\b)\ \ lgx=\dfrac{1}{2}\ \ ,\ \ x=10^{1/2}\ \ ,\ \ x=\sqrt{10}\\\\Otvet:\ \ x=\dfrac{\sqrt{10}}{10}\ ,\ x=\sqrt{10}\ .

ПОКАЗАТЬ ОТВЕТЫ
violet71 violet71  15.10.2020 16:27
ответ:

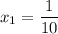x_1 = \dfrac{1}{10}; x_2 = 10

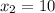
Объяснение: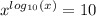

x^{log_{10}(x) } = 10\\

Найдём область допустимых значений.

ОДЗ: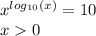 x^{log_{10}(x) } = 10\\x 0

Упростим уравнение.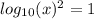

log_{10}(x)^{2} =1

Извлечём квадратный корень из обеих частей уравнения, не забывая об использовании положительных и отрицательных корней.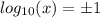

log_{10}(x) = \pm1

Разделим уравнение на 2 возможных случая.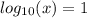

log_{10}(x) = -1

log_{10}(x) = 1

Решим относительно x.

x_1 = \dfrac{1}{10}\\x 0

x_2 = 10

x_1 = \dfrac{1} {10} \\\\x_2 = 10

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Nawrik34digma Nawrik34digma  03.09.2021 14:02
3. Найдите объединение и пересечение числовых промежутков продолжение: c) [-7; -1]; d) [-7;5]...
Hafs Hafs  03.09.2021 14:04
В 264 сначала нужно упростить выражение в левой части задачи......
машунька0811 машунька0811  03.09.2021 14:05
 Вычислите значение выражения только 1)...
назик31 назик31  03.09.2021 14:06
(1,8*0,4-2 9/15:6 1,3) : (-0,8)...
aicha21 aicha21  03.09.2021 14:08
Выполните указанные действия: а...
asurnakova156 asurnakova156  03.09.2021 14:08
14p 15q² (p-5)² 3p² 5q³ : 21p² 29°...
PesBarboss PesBarboss  03.09.2021 14:11
8. Сложите верные числовые неравенства: б) -2 -3 и 3 2; г) -8≤0 и 8≤9...
сказка500 сказка500  03.09.2021 14:13
26. Найдите неизвестный у из пропорции: 5 21 — у 1) 2) 5 30 6 28 40 - y 220 3) - 11 13 у – 49 21 78 14 4) 53 = 220 у + 300 ; = 29 5) 30 52 6) 4 y + 2 Зу – 2 33 13 7) 17...
botanchik1 botanchik1  03.09.2021 14:14
 Вычислите значение выражения только )...
hhhttt1520 hhhttt1520  03.09.2021 14:14
разобраться с этим только надо все расписано было...

Популярные вопросы