Показательные уравнения 3^(2х+1)=27+53*3^(х)+3^(2х)
Другие вопросы по теме Алгебра
Популярные вопросы
- Какие виды вегетативного размножения наиболее распространены в практике...
1 - Какие суффиксы у глаголов неопределенной формы?...
2 - Укажи цыфрами название водоемов. да искуственный водоем нет да соединяет...
1 - Какая начальная форма слова по ложбинке?...
2 - Найдите лишнее слово: 1) юстиниан, ника , храм святой софии, иконоборцы,...
3 - Как разобрать слово по составу подходила...
1 - Вклассе вместе с васей присутствует 25 учеников. на уроке биологии...
3 - А)косинус х -2 синус х=0 б)косинус в квадрате х +4 косинус х=0 в)синус...
3 - Какой тип имеют сша в начале 21 века?...
2 - Сколько здоровых хромосом у человека...
1
Пусть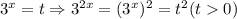
ответ: 3
2t²-53t-27=0;
D=2809+4*2*27=3025=55²;
t₁=(53-55)/4=-0,5; ∅ t>0;
t₂=(53+55)/4=27;