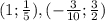Подскажите , решение этой системы уравнений по шагам.
Другие вопросы по теме Алгебра
Популярные вопросы
- Роль української пісні в повісті,, сліпий музикант в...
3 - До ть будь ласка треба коротка інформація про будь яку тварину яка живе в ПІВДЕННІЙ...
3 - Напряжение источника U = 12 В, внутреннее сопротивление ri = 10 Ом, сопротивление...
2 - Запишите название любого объекта (города, населённого пункта, реки или др.),...
3 - . Керісінше сөзжұмбақ». Созжұмбакта берілген жауаз сиздерди. сұрақ-тапсырмаларын...
2 - Знайди усі цілі числа, що задовольняють нерівність |x| 3,4. 2) Замість зірочки...
1 - Проблеми твору Сто тисяч . Відповідь обґрунтуйте...
3 - ПРОВЕРЬТЕ ВАШИ ЗНАНИЯ! 1. Какие вы знаете этапы и критерии принятия экономического...
1 - Докажи, что неравенство верно при всех значениях переменной. 0, 2(x + 3) - x...
2 - 3. Прочитай сказку, которую сочинила ученица. Определи тип текста (описание,...
3
Выражаем из второго уравнения
Подставляем в первое уравнение
Теперь решаем обычное уравнение (раскрываем скобки, убираем дробь и т.д.)
Домножим уравнение на 5, чтобы избавиться от дроби (смысл уравнения не меняется)
Так же и поделим уравнение на 2, чтобы проще было считать (смысл не меняется) и решаем уравнение
Теперь возвращаемся к и просто подставляем значения
и просто подставляем значения
ответ