Подскажите как решить: 1. 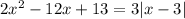
2. Найти сумму целых решений неравенства: 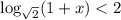
Другие вопросы по теме Алгебра
Популярные вопросы
- https://community.today.com/post/watchhd-made-in-italy-2020-online-full-movie-free...
2 - Какое минимальное число раз подряд надо записать число 1234 так, чтобы...
1 - Укажите предложение, в котором между подлежащим и сказуемым ставиться...
2 - Найдите значение выражению...
3 - подтвердить аккаунт в WeChat Кто-нибудь у кого есть WeChat, укажите...
1 - Малыш умножил два числа и записал полученное равенство. Карлсон вместо...
1 - Диагональ прямоугольной трапеции перпендикулярна длинной боковой стороне...
3 - Поставте замість зірочки такі Цифри щоб число 183** ділилось на 9...
1 - 480 км проїхали велесипедист мотоцикліст автомобіліст.їхня спільна...
2 - Сравнить дроби 21/16 и 21/11...
3
Объяснение:
1.
2x^2-12x+13=3*|x-3|.
Раскрываем модуль, получаем систему уравнений:
Решим первое уравнение:
Решим второе уравнение:
ответ: x₁=5,5 x₂=0,5.
2.
ОДЗ: 1+x>0 x>-1 ⇒ x∈(-1;+∞).
Учитывая ОДЗ: x∈(-1;1). ⇒
Одно целое решение: х=0
ответ: ∑=0.
Объяснение:
1) x≥3
2x^2 - 12x + 13 - 3x + 9 = 0
2x^2 - 15x+ 22 = 0
D = 225 - 4*2*22 = 49 = 7^2
x1 = (15 - 7)/4 = 2 ∉ x≥3
x2 = (15 + 7)/4 = 5,5
x<3
2x^2 - 12x + 13 - 9 + 3x= 0
2x^2 -9x + 4 = 0
D = 81 - 4*4*2 = 49 = 7^2
x1 = (9 - 7)/4 = 0,5
x2 = (9 + 7)/4 = 4 ∉ x<3
ответ: х = 0,5, х = 5,5
2) ОДЗ: 1 + x > 0, x > -1
2log2 (1 + x) < 2log2 (2) | :2
1 + x < 2
x < 1
С учетом ОДЗ: x ∈ (-1; 1)
-1 и 1 не входят в промежуток, т.к. знаки неравенства строгие, поэтому единственное целое число из этого промежутка это ноль
ответ: 0