Подробно решить уравнение

p.s. без полного раскрытия первых двух скобок и калькулятора (для решения такого рода уравнений).

Пусть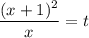 , тогда мы получаем

Рассмотрим функцию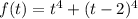 . Её производная функции: 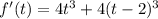. Приравнивая производную функции к нулю, мы получим

которое равносильно уравнению откуда

_____-____(1)____+_____

Функция убывает на промежутке t ∈ (-∞; 1), а возрастает - t ∈ (1; +∞). Следовательно, t = 1 — относительный минимум. Тогда f(1) = 2 и при этом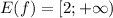 . То есть, t = 1 — решение уравнения 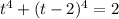и единственно.

Выполним обратную замену:

Дискриминант отрицателен, следовательно, квадратное уравнение действительных корней не имеет.

ответ: нет решений.