Подпишусь и сделаю лучшим ответом! 1. Какой порядок у числа
?
2. В каком из случаев число 1.560.000 записано в стандартном виде?
3. Запишите в стандартном виде.
а) 0,00476 б) 391×10^6 в) 0,086×10^-5
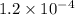
Другие вопросы по теме Алгебра
Популярные вопросы
- Порекомендуйте 3-4 сайта компаний, которые вам нравятся. рекомендуйте те компании,...
2 - Вчём сходство религии с древних египтян верованиями первобытных людей...
3 - Кто может придумать девиз? нужен девиз к названию паразиты...
2 - От каких слов произошли слова лиловый,оранжевый,фиолетовый?...
2 - Какое значение для организма имеет осуществление обмена веществ...
3 - Надо сочинить предложения со словами по ! helmet,basketball,gloves,bicycle,trainers,cap,guitar,digital...
3 - Тема предстоящего сочинения - «летние радости». напишите рассказ, озаглавьте...
3 - Какое количество теплоты выделилось при охлаждении золотой детали массой 560...
2 - Окружающий мир четвёртый класс номер четыре страница 15 самые высокие горы разных...
1 - Составьте 5-6 сложных загадок для 5-го класса. умаляю, ....
2
1. Какой порядок у числа 1.2 × 10^(-4)?
Для определения порядка числа в научной нотации нужно посмотреть на показатель степени (то, что находится после "× 10"). В данном случае, показатель степени равен -4. Положительное значение показателя степени увеличивает число, а отрицательное - уменьшает. Таким образом, число 1.2 × 10^(-4) меньше единицы, так как показатель степени отрицательный. Порядок данного числа составляет -4.
2. В каком из случаев число 1.560.000 записано в стандартном виде?
Стандартная форма записи числа представляет собой число от 1 до 9.99, умноженное на 10 в некоторой степени. Для определения, в каком из случаев число 1.560.000 находится в стандартной форме, нужно найти такую форму записи данного числа. Воспользуемся следующим алгоритмом:
а) 0,00476: данное число меньше 1, а значит не соответствует стандартной форме;
б) 391×10^6: в данном случае число представлено в форме числа от 1 до 9.99, умноженного на 10 в степени 6. Это стандартная форма записи числа 1.560.000;
в) 0,086×10^-5: данное число меньше 1, а значит не соответствует стандартной форме.
Таким образом, число 1.560.000 записано в стандартной форме в случае б).
3. Запишите число в стандартном виде.
Для записи числа в стандартной форме нужно перевести его в число от 1 до 9.99, умноженное на 10 в некоторой степени. Давайте рассмотрим каждый вариант:
а) 0,00476: данный вариант представлен в виде десятичной дроби меньше 1. Чтобы перевести его в стандартную форму, нужно сдвинуть запятую на 3 позиции вправо. Таким образом, число будет равно 4,76 × 10^(-3).
б) 391×10^6: данное число уже записано в стандартной форме.
в) 0,086×10^-5: аналогично варианту а), нужно сдвинуть запятую на 2 позиции вправо. Таким образом, число будет равно 8,6 × 10^(-7).
Надеюсь, я смог окончательно разъяснить вам эти вопросы. Если у вас возникнут еще вопросы, не стесняйтесь задавать их!