1. Алгебра
  2. ПО АЛГЕБРЕ Найдите сумму всех

ПО АЛГЕБРЕ Найдите сумму всех положительных членов арифметической прогрессии: 43; 39…

Gabela01 Gabela01    1   29.04.2020 17:27    7

Ответы
xawodilal xawodilal  14.10.2020 03:20

Объяснение:

И так первый член арифметической прогрессии равен 43, второй 39

a_{1} = 43

a_{2} = 39

Находим разность d =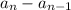 a_{n} - a_{n-1}  

d = a_{2} - a_{1} = 39-43= -4

нам нужно найти какой член самого наименьшего положительного числа?

a_{n} > 0

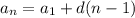
Формула a_{n} = a_{1} + d(n-1)

a_{1} + d(n-1) 0

43 - 4(n-1) > 0

47>4n

n<11.75

Наибольший член арифметической прогрессии равно n = 11 (только натуральное число)

a_{11} = a_{1} + d(n-1)

a_{11} = 43-4(11-1) = 3

и так осталось найти сумму всех положительных членов прогрессии

S_{n} = \frac{a_{1}+a_{n}}{2}*n

S_{11} = \frac{a_{1}+a_{11}}{2}*11 = (43+3)/2 * 11 = 253

253

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
svetaH666 svetaH666  07.12.2021 13:05
Не выполняя построение определи какие точки принадлежат графику функции по братски...
VADIMSTRENDG VADIMSTRENDG  07.12.2021 13:07
Упростить выражение 1) (4ху²-х+2х²у) - (2ху²+3х+2х²у)...
olenanuchajj8 olenanuchajj8  07.12.2021 13:07
только а б в г все до завтра надо...
gpatimat gpatimat  25.07.2019 12:10
3. найдите значение выражения: |3x − 25| + |3x + 25| при х = 7 a) 102 b) −172 c) 50 d) −50 4. сколько секунд в m минутах? a) 60m b) 360m c) 100m d) m + 60...
natashaevtushenko natashaevtushenko  25.07.2019 12:10
Найдите значения выражений 1) b³/b⁹*b⁵ при b=0,2 2) (3a³)³/(3a⁸) при a =110 3) 7x*(7x¹²)³/(7x⁹)⁴ при x=97...
прррр10 прррр10  25.07.2019 12:10
Найди равенства, которые являются тождествами. t^m⋅t^n=t^m+n (tm)^n=t^nm^n 3(t−m)=3t−3m t^5+t^2=t^5+2 −t−m=−(t+m) t^3−m^3=(t−m)(t^2+tm+m^2) (8m)^2=8m^2...
Lana8254 Lana8254  25.07.2019 12:10
Аж 45 за такое простое : d выражения: а) -х^3 y^2 + 2x^3 y^2 - 3x^3 y^2 (^ и число, следующее за ним - степень) б) (2ab^3)^4 : (2a^2 b) ^2 в) (n^8)^4 * n /(черта дроби) (n^3)^11...
anyanaffanya anyanaffanya  25.07.2019 12:10
Вычислите 2√16-√25 вот варианты ответов 1)4.5 2)3 3)18 4)4...
RETYUOP RETYUOP  25.07.2019 12:10
Запишите разность квадратов: (-5х) и 4у...
нануша456 нануша456  31.01.2022 12:20
Розкладіть на множники многочлен: 9x²y³-27x⁴y³+18x³y⁵...

Популярные вопросы