Пи интеграл от ^ 1 до -1 (1-x^2)dx
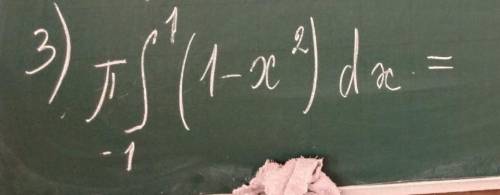
Другие вопросы по теме Алгебра
Популярные вопросы
- Почему в самой византии правители назывались ромейскими(римскими) императорами,...
1 - При или пре? вообще не понимаю эту тему( учителя, значение, , с другом,...
1 - Найти четырехзначное число,которое в 4 раза меньше числа, записанного теми...
3 - Составить на нахождение средней скорости если средняя скорость волги 40...
3 - Дети-цветы жизни, боец невидимого что это за выражения?...
1 - Найти обратную функцию к функции у=f(x) a) у=x2+1,x =0 b) y=(x-1)2, x =1...
3 - Катер первую половину пути со средней скоростью в 2 раза большей,чем вторую....
3 - Медный и фарфоровый шарики имеют одинаковую массу, сравните их объём, если...
3 - Разберите по составу слова: испугаться, порыгрывая, голубоглазый, небезопасный,...
2 - 1)x: 6,3=2целых одна седьмая : 1,25 2)4 целых четыре пятых : 0,8 = x : 1...
3
Объяснение:
Вычислим сначала неопределенный интеграл: