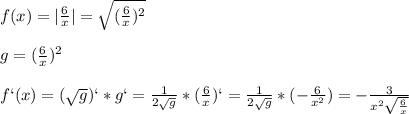 Photomath говорит, что правильный ответ будет
Photomath говорит, что правильный ответ будет 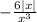 . Где я допустил ошибку?
. Где я допустил ошибку?
Другие вопросы по теме Алгебра
Популярные вопросы
- Составьте несколько новых пропорций из пропорции: 24 ÷8 = 4,8 ÷ 1,6 ;...
3 - Вримской республике (так же напишите какие были особенности)...
2 - Вместе с другом понаблюдай за ветром в течение 5-7 дней в одно и то же...
1 - Скласти речення зі словами бородавка, бюлетень, бурштиновий...
2 - Написать сочинение про прелести астаны на лист а4 на казахском языке 30...
3 - 34 разложите на множители квадратный трех член: / 2x²-9x+4...
1 - Что текст? ходить жовтень по краю та й виганяє птахів із гаю.осінь в україні...
3 - Написати твір за прислів ями. слова без діла - всеодно що гітара без струн....
1 - Среди данных чисел 5,7,35,105,150,175 выберите; а)делители 300....
1 - Определить степени сравнения прилагательных и сравнительную и превосходную...
2
Ошибка :
Вы забыли средний множитель