пешите уровнение со стиелками x²+2x-3 >0

Объяснение:

+2x-3>0

Это парабола, ветви вверх, нам нужны Х при которых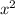 +2x-3 принимает только положительные значения, т.е 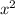+2x-3>0

1. Находим нули неравенства

+2x-3=0
D=4-4*(-3)=4+12=16

2) Чертим координатную прямую х, ставим найденные значения и видим, что неравенство принимает только положительные значения при

х∈(-∞;-3)∪(1;+∞)

так же можно разложить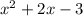 на множители, т.е.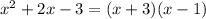

И решить через метод интервалов т.е