Первый, второй и третий члены геометрической прогрессии соответственно равны 2k+1; k + 2; 8 - k
а) Найдите значение k .
b) Найдите сумму бесконечно убывающей геометрической прогрессии.
Другие вопросы по теме Алгебра
Популярные вопросы
- На какой контурой карте можно увидеть рельеф украины...
3 - є невеликий моток мідного дроту, мірний циліндр з водою, олівець,...
3 - мне, напишите на карте и отправьте фото Африка Мысы : Мыс Игольный,...
2 - 3-тапсырма. Берілген сөйлемдерден жанаса байланысқан сөз тіркестерін...
2 - 2) значення аргументу, при якому значення функції дорівнює: 5,...
2 - Правильно записуючи прикладки. 1. У воєводи є дочка/красуня.2....
1 - Почему Риздвяна песня в прозе называла песней ? очень !!...
1 - Завдання 1.2. Розгляньте, як позначено і підписано гори на географічних...
2 - ответы на этом тест : 1. Внимание каких учёных привлекали былины?...
3 - Визначте причини суть і спрямованість нової економічної політики...
1
ответ: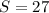 .
.
Так как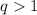 , то прогрессия не является бесконечно убывающей .
, то прогрессия не является бесконечно убывающей .