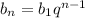Первый и девятый член прогрессии равны соответственно 135 и 5/3 найдите заключенные между ними члены этой прогрессии. распишите, как можно п одробно, что и как вы делаете, по какой формуле
Другие вопросы по теме Алгебра
Популярные вопросы
- Послідовність позначення ічного обєкта на контурній карті...
2 - Бічна грань правльної трикутної піраміди утворює з площиною основи кут 30°.радіус...
1 - Как достойно ответить на уверенна...
3 - T^2-6t-5=2 найти время материальной точки...
3 - Кто сидел в пруду в произведении крошка енот ?...
1 - Какая основа предложения : алексей по-звериному чувствовал,что кто-то внимательно...
1 - Представим, что у нас есть путешественники в первый день они во второй 19,...
2 - Составить 5 условных предложений на языке желательно по скорее....
1 - Положительные и отрицательные проявления ....
2 - Как объяснить, что из1/200 части тела востанавливается целый организм гидры...
2
используем формулу n-го члена геометрической прогрессии