1. Алгебра
  2. Первый член прогрессии

Первый член прогрессии равен 1 ,сумма 3 и 5 членов равна 90.найдите сумму первых 5 членов.

dashaKrylova41 dashaKrylova41    3   29.05.2019 15:20    1

Ответы
vladik883763 vladik883763  28.06.2020 18:59

По формуле n-го члена геометрической прогрессии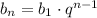 b_n=b_1\cdot q^{n-1}


b_3+b_5=b_1q^2+b_1q^4=90

Подставляя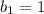 b_1=1, получим биквадратное уравнение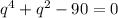 q^4+q^2-90=0

И решим это биквадратное уравнение как квадратное уравнение относительно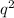 q^2.

Из теоремы Виета: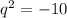 q^2=-10 - решений не имеет

                                  q^2=9   откуда  q=\pm3


Найдем сумму первых пяти членов геометрической прогрессии:

Для q = 3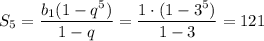

            S_5=\dfrac{b_1(1-q^5)}{1-q}=\dfrac{1\cdot(1-3^5)}{1-3}=121

Для q = -3

             S_5=\dfrac{b_1(1-q^5)}{1-q}=\dfrac{1\cdot(1-(-3)^5)}{1-(-3)}=61

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
ПЛЮШЕВЫЙМШКА1 ПЛЮШЕВЫЙМШКА1  12.08.2019 10:50
Найти значение выражение - 7 × 12 : ( - 5-1 )...
Tapoocek Tapoocek  12.08.2019 10:50
−4,4−(−0,67)−3,73−10,138−0,67−(−4,4)= ?...
korolevalena20 korolevalena20  25.03.2019 00:50
Решите неполное квадратное уравнение: х2+5х=0; 4х2-х=0; х2-15х=0; 4х2-20=0; 192-1/3х2=0...
Potashka Potashka  24.03.2019 15:30
Просто ничего не понимаю, 3 делать не надо...
леракулдошина леракулдошина  24.03.2019 15:29
Выражение 5ab•a²•14(ab²)²=• точка это умножение​...
HelpFox HelpFox  25.03.2019 00:50
2.решите систему неравенств 5-3х˃ 15+2х, 3+7х 4х 3.постройте график функции у= -6х+5. укажите, при каких значениях х значения у˃0; у 0. 5.завод должен был изготовить...
XuJIuGan XuJIuGan  25.03.2019 00:50
Сократите дробь х3-3х2-4х+12 деленое (х-3)(х+2) решение...
egyrt egyrt  25.03.2019 00:50
Постройте график функции y= sin^2 квадратный корень x^2-4 + cos^2квадратный корень x^2-4...
mixakov05 mixakov05  24.03.2019 15:25
Квадрат разделен на 10 маленьких равных прямоугольника. найдите площадь маленького квадрата равна 19 см². решение ! ​...
AnektodaNet AnektodaNet  25.03.2019 00:50
33 корень из 2*cos(495) 24 корень из 3*tg(-1020) 10 корень из 6*cos(-п/4)*sin(-п/3) -22 tg14*tg104 11/ sin^2 50+sin^2 140...

Популярные вопросы