Первые 3 задания Более подробно распишите
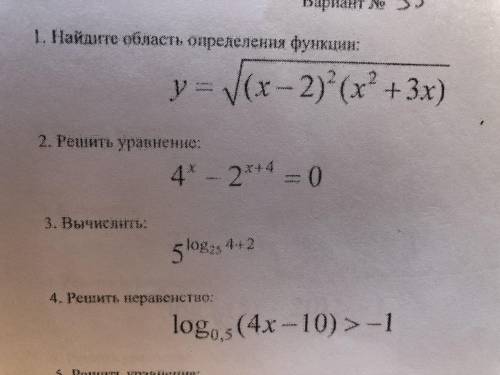
Другие вопросы по теме Алгебра
Популярные вопросы
- Проложите по карте наиболее удобный путь хаджа правителя Мали Канку Мусы....
2 - Пирамида майя в Чичен-Ице. XII—XIII вв. Какие народы Древнего мира строили похожие...
3 - Определите географическое положение территорий расселения инков, ацтеков и майя....
3 - С какой стороны в Индию вторгались завоеватели? Какой из торговых путей на карте...
3 - Составьте сравнительную таблицу «Страны средневековой Азии»....
3 - В какие известные вам государства в период Средневековья входили территории...
2 - Как вы считаете, кастовый строй мешал или развитию Индии?...
2 - Что вы знаете о плавании викингов к берегам Америки? Почему это открытие осталось...
1 - Подготовьте рассказ о технологии изготовления изделия из фарфора, шёлка, производства...
3 - Когда и кем было создано первое единое государство в Китае, в Индии?...
1
========================================
Объяснение:
1)(-inf, -3] объединить с [0, inf)
2)4
3)50.
Объяснение:
1) Значение под корнем должно быть ≥0, (х-2)^2 всегда ≥ 0 => (х^2+3х) ≥ 0 => х(х+3) ≥ 0 нули: 0, -3 => x принадлежит (-inf, -3] объединить с [0, inf)
2) Запишем в виде 2^(2х) - 2^(х+4) = 0 => 2х = х+4 => х=4
3) По свойствам логарифмов:
5^(log25(4)+2) = 5^(0.5*log5(4)+2) = 5^(log5(4^(0.5))+2) = 5^(log5(2)+2) = 25*5^(log5(2)) = 25*2 = 50