Первообразная ∫(2sinx+4x7)dx Выберите один ответ:
a. 2cosx+x8/2+C
b. -2cosx+4x8+C
c. -2cosx+x8/2+C
d. 2cosx+28x6+C
Другие вопросы по теме Алгебра
Популярные вопросы
- 22 грудня в києві день триває 8 год. скільки годин у цю добу триває...
2 - Часть российской империи, имевшая в середине хiх в. свои парламент,...
3 - По тарифному плану «просто как день» компания сотовой связи каждый...
2 - Сравни а)1,8 и 1,089 б)21,56и 2,561...
3 - 4класс! выпиши по группам слова известных вам частей речи.(типо имя...
1 - За два пакета молока и пачку творога заплатили 59рублей. пачка творога...
3 - {x+2*y =12 {2*x-3*y=-18 решите уравнение сложения...
1 - 2. смешали 20 г сахара и 250 мл воды. какова массовая доля сахара...
2 - Мини сочинение на тему легко ли быть учеником на уровне 7 класса...
3 - Втреугольнике авс стороны ас и вс равны. внешний угол при вершине...
2
Проинтегрируем каждый член отдельно, а затем запишем в общий вид:
Теперь запишем в общий вид. Это и будет ответом.
Использованные формулы:
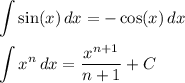
ответ: