1. Алгебра
  2. Периметр прямоугольника 50

Периметр прямоугольника 50 см. Найди его стороны, если площадь прямоугольника равна 156 см²

Pikasso07 Pikasso07    2   18.01.2022 06:06    1

Ответы
мпрлкт мпрлкт  18.01.2022 06:10

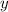Пусть стороны равны x и y. По условию:

\begin{cases}2(x+y)=50\\xy=156\end{cases}\\\begin{cases}x+y=25\\xy=156\end{cases}\\y=25-x\\x(25-x)=156\\25x-x^2=156\\x^2-25x+156=0\\D=(-25)^2-4 \cdot 156=625-624=1\\x_1=\dfrac{25+1}{2}=13; \qquad x_2=\dfrac{25-1}{2}=12

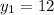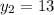Понятно, что система уравнений симметрична относительно переменных, поэтому: y_1=12 и y_2=13 (если непонятны рассуждения, найдите игреки по формуле y=25-x).

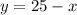ответ: 13 и 12 см.

Проверка:

P=2 \cdot (13+12)=2 \cdot 25=50\\S=13 \cdot 12=156

Соответствует условию.

Что-нибудь непонятно? Спрашивай, с удовольствием объясню.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
arinashemetova arinashemetova  25.04.2020 14:46
Для линейного уравнения 4x+5y-20=0 найдите значение x, если y=0....
Анкта Анкта  25.04.2020 14:46
нужно- обосновать свой ответ, решением каждого неравенства,графически методом нужно ​...
krisvll krisvll  25.04.2020 14:46
Для покраски 1 м2 потолка требуется 220 г краски. Краска продается в банках по 2 кг. Сколько банок краски нужно купить для покраски потолка площадью 34 м2?...
саша17101 саша17101  25.04.2020 14:47
Разложи на множители: 196g−gu2...
vovachetaikin86 vovachetaikin86  25.04.2020 14:47
Производные функции решить Много...
danaj04 danaj04  25.04.2020 14:47
Как найти корень этого уравнения?...
konton konton  25.04.2020 14:47
Розв яжіть рівняння: 1) (х-6)^-корень 3=3 2) (х+4)^корень 5=а 3) (х-1)^-корень 7=а...
belka1006 belka1006  25.04.2020 14:47
В одной коробке 10 тетрадей, 2 из которых в клетку, а в другой – 8 тетрадей, 2 из которых в клетку. Из коробок вынули по одной тетради. Какова вероятность того, что...
adidok199680 adidok199680  11.04.2021 09:45
Может кто-нибудь решить скинули а у меня времени нет ​...
наргиз68 наргиз68  11.04.2021 09:43
 Дано квадратное уравнение x^2+10,5-1=0, укажите сумму и произведение Корней x1+x2= x1•x2=...

Популярные вопросы