Пассажирский поезд должен пройти с постоянной скоростью расстояние между станциями, равное 312 км. когда он половину расстояния, то был задержан на светофоре на 12 минут, поэтому, чтобы наверстать опоздание машинист увеличил скорость поезда на оставшемся участке пути на 5 км в час. с какой скоростью поезд шел после остановки? ( нужно решить по теореме виета)
Другие вопросы по теме Алгебра
Популярные вопросы
- Расположите в порядке увеличения0,5кг 5000г 50.000мг 0.05т...
3 - 2.послушать 2 разных марша и сравнить их звучание....
3 - Выписать из рассказа корзина с еловыми шишками эпитеты и олицетворение...
1 - Составить сложные предложения с союзами: в силу того что, пока, покуда, вследствие...
1 - V1=v2=v3 h=0,2 м pводы=1000 кг/м3 ркеросина =800кг/м3 рртути=13600кг/м3 найти давление...
1 - Вы мне ответ, а я вам от чистой души, по братски.бак наполняеться через краны a...
1 - Какие массы соли и воды необходимо взять для приготовления 260 грам 25%- ного раствора....
3 - Запустите интегрированную среду программирования . составьте программный код для...
1 - (х-1)^2*(х-3)=(х-1)^2 (х^2-2х+1)*(х-3)=х^2-2х+1 а дальше? ? не могу понять как перемножить,...
2 - Кем же на самом деле была стрекоза из басни стрекоза и муравей ? текст: знаменитая...
2
ответ: 65 км/ч
Объяснение:
1) 312 : 2 = 156 (км) - половина расстояния
2) 12 мин = 12/60 ч = 1/5 ч
Скорость Время Расстояние
До остановки x - 5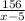 156
156
После ост. x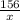 156
156
Время до остановки на 12 мин больше времени после остановки:
х > 5 по смыслу задачи, поэтому умножим обе части уравнения на
5x(x - 5):
780x - 780(x - 5) = x(x - 5)
780x - 780x + 3900 = x² - 5x
x² - 5x - 3900 = 0
По теореме Виета:
x₁ · x₂ = - 3900
x₁ + x₂ = 5
Значит, x₁ = - 60 - не подходит по смыслу задачи
x₂ = 65
ответ: 65 км/ч