ответы без решения не принимаются
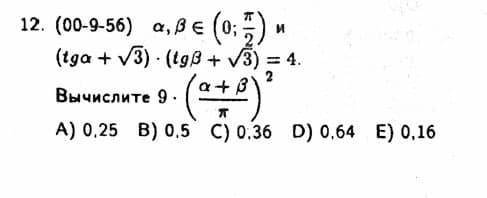
Другие вопросы по теме Алгебра
Популярные вопросы
- Доклад на тему: я в обществе я в коллективе...
2 - 2(3-x)+7x=4-(3x+2) уравнение. зарание !...
1 - 50 какие сельскохозяйственные растения вы знаете на зко вко ско...
1 - Составьте и запишите две компьютерных программы на языке программирования...
2 - 5діє слів и через - перевести в минулий час спөсибө зарание 15...
2 - 4класс. каждый из 425 рабочих заводов изготавливаются по 236...
3 - Какое число надо вписать в окошко, чтобы равенство стало верным?...
3 - Сумка с продуктами весит 4 килограмм 200 грамм в ней 3 пакета...
2 - №1 в равнобедренном треугольнике авс основание ас равно 12 см,...
2 - Расположите части так, что бы получился связной текст. озаглавьте...
2
A)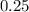
Объяснение:
Вспомним:
__
Узнаем чему равен угол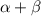 :
:
Так как
то
и
__
Вычислим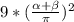 :
: