Алгебра: Отметьте на координатной прямой число 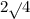ответ:7891011141213

Для решения этого вопроса нужно понимать, как размещать числа на координатной прямой и как работать с корнями. На координатной прямой каждой точке соответствует определенное число. Используя числа, мы можем указать позицию на координатной прямой. Дано число . Разберемся, что это число означает. - это запись выражения, в котором указывается корень, а внутри корня находится число 4. Итак, наша задача - найти, на каком месте на координатной прямой расположено это число. Чтобы найти его положение, мы...

Отметьте на координатной прямой число $2 \sqrt{ } 4$

ответ:
7
8
9
10
11
14
12
13

Ответы

9102936435 26.01.2024 09:13

Для решения этого вопроса нужно понимать, как размещать числа на координатной прямой и как работать с корнями.

На координатной прямой каждой точке соответствует определенное число. Используя числа, мы можем указать позицию на координатной прямой.

Дано число $2 \sqrt{ } 4$ . Разберемся, что это число означает.

$2 \sqrt{ } 4$ - это запись выражения, в котором указывается корень, а внутри корня находится число 4.

Итак, наша задача - найти, на каком месте на координатной прямой расположено это число.

Чтобы найти его положение, мы должны знать, какое число соответствует каждой позиции на координатной прямой.

Обычно на координатной прямой начало отсчета соответствует числу 0, а число увеличивается по мере движения вправо и уменьшается по мере движения влево.

Чтобы решить эту задачу, нужно оценить, где могло бы находиться число $2 \sqrt{ } 4$ .

Исходя из того, что под знаком корня находится число 4, можно предположить, что это число между числами 2 и 3. Потому что 2^2 = 4, а 3^2 = 9.

Теперь нужно определиться: должно ли число $2 \sqrt{ } 4$ быть больше или меньше 3.

Для этого возьмем два кандидата на решение: 2^2 = 4 и 3^2 = 9.

Нам нужно найти число, которое находится между 2 и 3.

Чтобы это сделать, можно возвести каждое число в квадрат и сравнить.

2^2 = 4 < $2 \sqrt{ } 4$ < 3^2 = 9

Из этого следует, что число $2 \sqrt{ } 4$ должно быть больше 2 и меньше 3.

Теперь, вернемся к исходному вопросу и посмотрим на возможные ответы.

7
8
9
10
11
14
12
13

Мы знаем, что число $2 \sqrt{ } 4$ больше 2 и меньше 3.

Сравним его со всеми ответами.

7 - больше 2, не подходит.

8 - больше 2, не подходит.

9 - больше 3, не подходит.

10 - больше 3, не подходит.

11 - больше 3, не подходит.

14 - больше 3, не подходит.

12 - больше 3, не подходит.

13 - больше 3, не подходит.

Исходя из этого, единственный ответ, который подходит, это число 3.

Таким образом, число $2 \sqrt{ } 4$ находится на координатной прямой в позиции 3.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра