Остатки от деления многочлена p(x) на x-1 и x+1 равны соответственно 1 и -7. найти остаток от деления этого многочлена на x^2-1
Другие вопросы по теме Алгебра
Популярные вопросы
- Верны ли суждения о кремниевой кислоте? А. Кремниевую кислоту можно получить...
3 - Найди верное объяснение отсутствия Ь в словах (пара) лыж, ( несколько ) задач...
1 - Круговая мишень радиуса 12 см разделена 5 концетрическими окружностями радиус...
3 - Ещё раз привет. Не подскажите как решить это уравнение (3x-5)-(7--4x)=2? Заранее...
3 - Написать реакцию этерификации карбоновой кислоты (на выбор, кроме той, которая...
2 - При каких значениях x двучлен 8x−9 принимает положительные значения?...
1 - Эсир поэтан хаш-хаш хайлавёсене вулана? Килешpёс-и весемсире?Ку саввӑн хаш йёрки...
1 - Не то крик птицы не то взмах крыльев рассёк тишину раннего утра. чем осложнено...
3 - Съезд князей в Любече считается историками условной датой начала периода ?...
2 - Причастие победившем что это такое и как оно образовано...
2
Пусть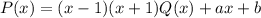
1)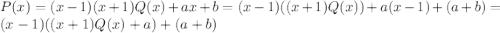 Тогда, по теореме Безу,
Тогда, по теореме Безу, 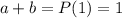 →
→ 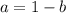
2)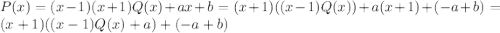 Тогда, по теореме Безу,
Тогда, по теореме Безу, 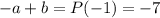 →
→  →
→  →
→ 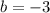 →
→ 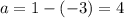
3) Тогда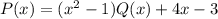 → Остаток от деления
→ Остаток от деления 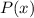 на
на 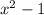 равен
равен 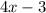
ОТВЕТ: 4x-3
Запишем согласно теореме Безу:
P(x)= (x-1)*g(x) +1
P(x)=(x+1)*f(x)-7
p(x)*(x+1)=(x^2-1)*g(x) +(x+1)
p(x)*(x-1)=(x^2-1)*f(x)-7*(x-1)
Вычитаем оба равенства:
2*p(x)=(x^2-1)*(g(x)-f(x)) +8x-6
p(x)=(x^2-1)*( (g(x)-f(x))/2 ) +4x-3 (4x-3 не делится на x^2-1 тк его степень ниже)
ответ: остаток 4x-3