Определите, является ли функция возрастающей или убывающей: 1)у=√5^x 2) y=1\√5^x 3)y=(3\2-√2)^x 4)y=(2\3-2√2)^x 5)y=(π\3)^x 6) y=(3\π)^x 7) y=(4-√7)^x 8)y=(4+√7\9)^x , с полным решением!

Ответы

mixtalalai2017 14.06.2020 09:42

Нам нужно оценить основание - то, что возводится в степень. Если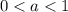 0<a<1 , то функция убывает. Если 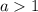, то воз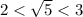растает.

1) $2<\sqrt{5}<3$ - возрастает

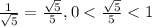2) $\frac{1}{\sqrt{5}}=\frac{\sqrt{5}}{5}, 0<\frac{\sqrt{5}}{5}<1$ - убывает

3)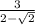 $\frac{3}{2-\sqrt{2}}$ . Умножим на число, сопряженное знаменателю
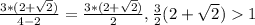$\frac{3*(2+\sqrt{2})}{4-2}=\frac{3*(2+\sqrt{2})}{2}, \frac{3}{2}(2+\sqrt{2})1$ - возрастает

4) Так же умножим на число, сопряженное знаменателю
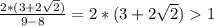$\frac{2*(3+2\sqrt{2})}{9-8}=2*(3+2\sqrt{2})1$ - возрастает.

5)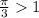 $\frac{\pi}{3}1$ , так как 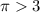$\pi 3$ . Значит функция возрастает.

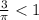6) $\frac{3}{\pi}<1$ - мы получим, если обратим обе части в примере выше. То есть, функция убывает.

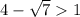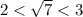7) $4-\sqrt{7}1$ , так как $2<\sqrt{7}<3$ . Функция возрастает.

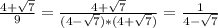
8) $\frac{4+\sqrt{7}}{9}=\frac{4+\sqrt{7}}{(4-\sqrt{7})*(4+\sqrt{7})}=\frac{1}{4-\sqrt{7}}$
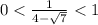$0<\frac{1}{4-\sqrt{7}}<1$ - это мы получим из примера выше. Значит, функция убывает.