Определите три правильные утверждения. 1. Пять разных книг можно расставить на полке 120 различными
2. Если вероятность купить бракованный ноутбук равен 0,005, то в любой партии с 1000 ноутбуков гарантированно есть 5 бракованных ..
3. Для выборки из четырех числовых данных: 2, 5, 8, 11 каждое из этих чисел является модой данной выборки.
4. Функция F (x) = 2х³ + 4х - соs2 является первоначальной для функции f (x) = 6х² + 4 + sin2.
5. ∫6sin (2х + 3) dх = - 6соs (2х + 3) + С
6. Функция F (x) = 1 / x² является первоначальной для функции f (x) = - (2 / x³) на промежутке (-2; 2).
7. Если ⁴∫₋₁ f (x) dх = 6, то ⁴∫₋₁ (f (х) - 1) dх = 1.
(Визначте три правильні твердження.
1. П'ять різних книжок можна розставити на полиці 120 різними
2. Якщо ймовірність купити бракований ноутбук дорівнює 0,005, то у будь-якій партії з 1000 ноутбуків гарантовано є 5 бракованих..
3. Для вибірки з чотирьох числових даних: 2, 5, 8, 11 кожне з цих чисел є модою даної вибірки.
4. Функція F(х) = 2х³ + 4х – соs2 є первісною для функції f( х) = 6х² + 4 + sin2.
5. ∫6sin( 2х + 3)dх = – 6соs(2х + 3) + С.
6. Функція F(х) = 1/x² є первісною для функції f( х) = –(2/x³) на проміжку (–2; 2).
7. Якщо ⁴∫₋₁ f(х)dх = 6, то ⁴∫₋₁ (f (х) – 1)dх = 1. )
Другие вопросы по теме Алгебра
Популярные вопросы
- Леңнің әр шумағындағы ойды сызба түрінде жаз. м. жұмабаев пен н. аитовтың...
1 - 10-тапсырма. жағдаят: iнiң фантастикалық шығарма оқығысы келетінінайтып,...
2 - 3^x+2/4=5^x+2 2^x^2-6x+0.5=1/16√2- показникові рівняння...
2 - Лттық киім тігетін фабрика үш күнде 98 киім дайындалады 2 күні 1 күнге...
2 - Как решать эти уравнения? заболела в начале года и уже нифига не понимаю....
1 - 64. 1) 9× (21 - 8); 2) 31 ×(5 - 9); 3) (40 - 29) ×12; 4) (51 - 15)...
1 - Complete the table with the in the box aren t sam m notls reisn tare...
1 - B,e,l,t,t,a,i,e,m какое слово может быть...
2 - Назовите основные уровни организма человека...
2 - Чудовище, с которым пришлось столкнуться гераклу описание чудовища...
1
2) Если утверждение равно, то вероятность того что среди 1000 ноутбуков будет 5 бракованных равна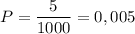 , верно
, верно
3) Не верно, ведь мода - число, которое наибольшее повторяется, а у нас все повторяются 1 раз.
4)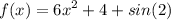 уже видно что sin(2)=const , а в первообразной виден cos(2) что не верно
уже видно что sin(2)=const , а в первообразной виден cos(2) что не верно
5)
6)
поэтому функция F(x)=1 / x² не является первообразной на для функции f(x) на промежутке (-2;2)
7) К примеру
верно.
1,2,7 - верные