Определите область допустимых значений и решите его как квадратное уравнение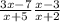
между ними равно

Решение силой Разума - Не допускается деление на ноль.

Решение.

a).

3 - х ≠ 0 или  х≠ 3 - первая дробь

(x² - 9) = (x-3)*(x+3) ≠0 х ≠ -3, х ≠ 3 - вторая дробь.

В третьей дроби всегда положительное число.

ОТВЕТ: ОДЗ: х ≠ -3,  х≠ 3.

б)

Решаем квадратные уравнения в знаменателях.

x² - 2x - 15 = 0 - уравнение в знаменателе первой дроби.

Находим дискриминант

D = (-2)² - 4*1*(-15) =  64,  √64 = 8, корни: x₁ = -3, x₂ = 5.

х² + 8х + 15 = 0 - уравнение в знаменателе второй дроби.

D = 8² - 4*1*15  = 4,  √4 = 2, корни: x₃ = -3, x₄ = -5

Значения при которых знаменатель становится равным 0 исключаем из ОДЗ. Значение х = - 3 - общее.

ОТВЕТ: ОДЗ: Х≠ -5 ; Х≠ -3; Х≠ 5

2а)  ОДЗ: Х≠ 1 - ответ

2б)  ОДЗ: Х≠ 0; Х≠ 3 - ответ.

Объяснение:

ОДЗ: х≠-5 и х≠-2

по правилу пропорции получим

(х-3)(х+5)=(х+2)(3х-7)

(х-3)(х+5)-(х+2)(3х-7)=0

х²+5х-3х-15-(3х²-7х+6х-14)=0

х²+5х-3х-15-(3х²-х-14)=0

х²+5х-3х-15-3х²+х+14=0

-2х²+3х-1=0; Д=3²-4*(-2)*(-1)=

=9-8=1; х1=(-3-1)/(-4)=(-4)/(-4)=1

х2=(-3+1)/(-4)=(-2)/(-4)=2/4=1/2

ответ: х=1 и х=1/2. оба корня подходят по одз.