1. Алгебра
  2. Определить вид кривой

Определить вид кривой второго порядка, построить её, найти вершины и фокусы. х^2+25y^2=25, y^2-24x=0, 2x^2-5y^2=10

hdbhbd hdbhbd    2   31.03.2019 02:30    1

Ответы
svetusik214 svetusik214  27.05.2020 20:17

Найдём инвариант кривой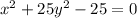 x^{2}+25y^{2}-25=0

Delta=\left[\begin{array}{ccc}1&0&0\\0&25&0\\0&0&-25\end{array}\right] = 1*(25*(-25)-0)=-625\neq0 => кривая невырожденная

D= \left[\begin{array}{ccc}1&0\\0&25\\\end{array}\right] = 1*25=250

I=1+25=26

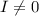Delta* I\neq0 => кривая центральная

D0 и Delta*I<0 => кривая - эллипс

 

 

Найдём инвариант кривой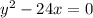 y^{2}-24x=0

Delta=\left[\begin{array}{ccc}0&0&-12\\0&1&0\\-12&0&0\end{array}\right] = (-12)*(0-1(-12))=-144\neq0 => кривая невырожденная

D= \left[\begin{array}{ccc}0&0\\0&1\\\end{array}\right] = 0

I=0+1=1

D=0 => кривая - парабола

 

 

Найдём инвариант кривой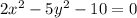 2x^{2}-5y^{2}-10=0

Delta=\left[\begin{array}{ccc}2&0&0\\0&-5&0\\0&0&-10\end{array}\right] = 2*((-5)*(-10)-0)=100\neq0 => кривая невырожденная

D= \left[\begin{array}{ccc}2&0\\0&-5\\\end{array}\right] = 2*(-5)=-10<0

I=2+(-5)=-3

Delta* I\neq0 => кривая центральная

D0 => кривая - гипербола

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
mussa777772 mussa777772  13.09.2019 07:50
Принадлежит ли графику функции y=1/x точка:...
malina2017 malina2017  13.09.2019 07:50
Найдите значение выражения (3√2)² 1) 6 2) 12 3) 18 4) 36...
Zhuldyzovazarina Zhuldyzovazarina  13.09.2019 07:50
Сравните значения выражений: 2√6 и 4√2. объясните почему получается 24 и 32?...
vprasckowya vprasckowya  13.09.2019 07:50
Корень 3 одна шестнадцатых умножить на 2 четырнадцать двадцать пятых...
Немножко000Фетешист Немножко000Фетешист  13.09.2019 07:50
Построить график функций в одной системе координат y=-3x ; y=2...
goddessshi goddessshi  14.08.2019 12:50
1) y=5x^5-sinx 2) y=5x^6+cosx найди производную...
vanyaburundukov vanyaburundukov  14.08.2019 12:50
Оцените периметр равнобедренного треугольника с основанием aсм и боковой стороной b cм,если 30...
olykharkov olykharkov  14.08.2019 12:50
1) высота равнобедренной трапеции, проведённая из вершины c, делит основание ad на отрезки длиной 10 и 11 найдите длину основания bc. 2) в параллелограмме abcd диагональ ac является...
HET228 HET228  14.08.2019 12:50
Х2/5-2х/3=х-5/6 / - дробная черта х2 - икс во второй степени...
19791207the 19791207the  14.08.2019 12:50
На каком расстоянии в метрах от фонаря стоит человек ростом 2 метра если длина его тени тени равна 1 метр высота фонаря 9 метров...

Популярные вопросы