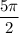Определить наименьший положительный период функции y=5 cos4/5x
Другие вопросы по теме Алгебра
Популярные вопросы
- Решите задание по геометрии 7 класс...
3 - Окончания какие здесь? Менің гүл. Сенің гүл ...
3 - Вставь пропущенные даты и расставь в хронологической последовательности 1....
2 - График линейной функции пересекает оси координат в точках (-5; 0) и (0; 11)....
2 - С примером Пять девятых икс плюс семнадцать девятых=две девятых икс плюс...
3 - Определите по карте,,Транспорт Казахстана’’в каких частях Казахстана представлены...
1 - Проверочная работа I. Раскройте скобки, поставьте глагол в Present Simple...
1 - Параграф 45 обьеденение и пересечение множеств...
2 - Что такое Марки? Тема: Империя Карла Великого...
1 - Как соединить эти слова правильно...
2
Применим формулу: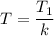 , где
, где 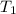 - период данной элементарной функции,
- период данной элементарной функции, 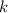 - коэффициент при
- коэффициент при 
Итак, период функции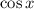 равен
равен 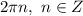 , а коэффициент функции
, а коэффициент функции 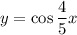 при
при  равен
равен  . Следовательно, период заданной функции равен
. Следовательно, период заданной функции равен 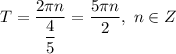
Наименьшим положительным периодом данной функции будет при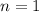 , то есть
, то есть 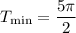
ответ: