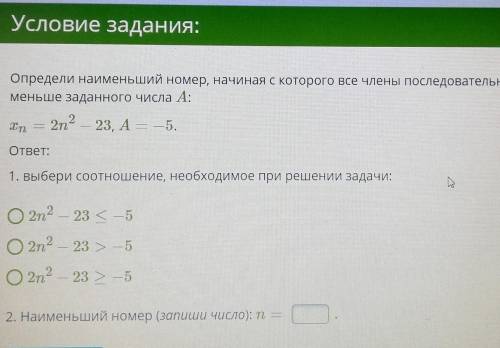
Определи наименьший номер, начиная с которого все члены последовательности (xn) будут не меньше заданного числа A:
xn=2n2−23, A=−5.
ответ:
1. выбери соотношение, необходимое при решении задачи:
2n2−23≤−5
2n2−23>−5
2n2−23≥−5
2. Наименьший номер (запиши число): n=
Другие вопросы по теме Алгебра
Популярные вопросы
- 170В. Можно ли назвать этот текст сказкой? Почему? Определи стиль...
1 - Найдите производнуюe^sinx*tg1/x...
2 - Какая сила препятствует спортсмену преодолеть планку на высоте 2 метра?...
3 - 6 Work in pairs. Imagine you are booking tickets for a concert or...
3 - Найдите предел/ Пределинтапкыла lim(x- ) (3(x+3x^2)/(x+2)=)...
1 - Задание для самостоятельной работы 1. Определить величину и направление...
2 - Уға болатын Соңғы кезде атмосферада -көп бөлінуде. Көмірқышқылболып...
2 - 3-тапсырма. Мәтінді оқып, түсіндіріп айт. Бөлек, дефис арқылы жазылғансөздерге...
2 - Какая роль в балетном спектакле принадлежит дирижёру симфонического...
3 - ПТМС формуласы бойынша Ә.Бөкейханов...
1
Шаг 1: Выберите соотношение, необходимое при решении задачи.
Мы должны выбрать соотношение, которое говорит нам, что все члены последовательности (xn) будут не меньше заданного числа A = -5. В данном случае, это будет 2n^2 - 23 ≥ -5.
Шаг 2: Решим неравенство 2n^2 - 23 ≥ -5.
Добавим 23 к обеим сторонам неравенства:
2n^2 ≥ 18.
Разделим обе стороны неравенства на 2:
n^2 ≥ 9.
Шаг 3: Найдем наименьшее значение n.
Учитывая, что n - целое число, наименьшее значение n будет 3. Потому что 3^2 = 9 и это первое число, с которого все последующие значения будут не меньше.
Ответ: Наименьший номер, начиная с которого все члены последовательности (xn) будут не меньше заданного числа A = -5, равен n = 3.