Определи наименьший номер, начиная с которого все члены последовательности (xn) будут не меньше заданного числа A: xn=4n2−34, A=−5.
1. выбери соотношение, необходимое при решении задачи:
4n2−34≥−5
4n2−34≤−5
4n2−34>−5
2. Наименьший номер (запиши число): n=
Другие вопросы по теме Алгебра
Популярные вопросы
- 3.1 Почему в исторической науке принято считать началом действия Великого Шелкового...
1 - Определить скорость тела, движущейгося по окружности радиусом 40000 см с ускорением...
3 - Что за приборы на рисунках? Как эти приборы используют и что измеряют? Cop...
1 - Напишите письменную работу публицистического стиля (репортаж) на одну Интересный...
3 - ::А. 30Б. 48В. 100Г. 24Д. 60...
2 - А. «Тәуелсіздік жылдарындағы Қазақстан. ЭКСПО-2017» бөлімі бойынша алған білімдеріңді...
2 - В колоді 52 карти. Навмання виймають чотири карти. Яка ймовірність того, що: а)...
2 - Вопрос по произведению отцы и дети С кем базарова свела учеба, и откого он подхватил...
3 - 2. Какова главная тема рассказа «Мальчик у Христа на ёлкен? a) страдания ребёнка...
1 - Используя формулу ПОПС, обоснуйте мнение о том, что культурно-генетический код...
2
Объяснение:
Не меньше - значит больше или равно (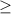 ):
):