Определи координаты точки числовой окружности
P(π/3) =
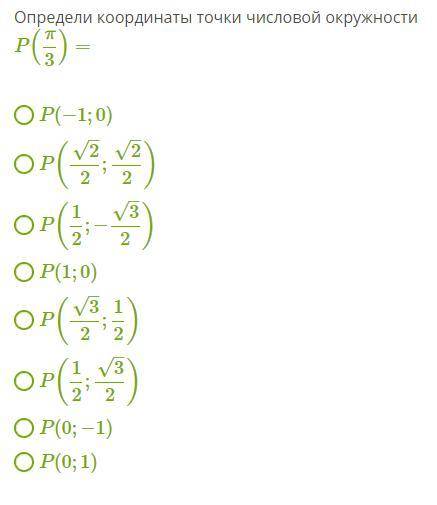
Ответы
Для определения координат точки P(π/3) на числовой окружности, мы должны понять, как устроена эта окружность и как связаны ее координаты с углом π/3.
Числовая окружность - это окружность радиусом 1, расположенная в декартовой системе координат. Центр окружности находится в точке (0,0), которую обычно называют началом координат.
На числовой окружности есть специальные углы, называемые терминальными углами, которые характеризуются своим расположением на окружности. Эти углы измеряются в радианах и соответствуют доле длины окружности.
Для нахождения координат точки P(π/3), мы смотрим на угол π/3 на окружности и строим прямую, проходящую через эту точку и центр окружности (0,0). Получается прямая, которая пересекает единичную окружность в точке P.
Чтобы найти координаты точки P(π/3), мы можем использовать формулы преобразования полярных координат в декартовы координаты. Эти формулы выглядят следующим образом:
x = r * cos(θ)
y = r * sin(θ)
где:
x и y - декартовы координаты точки P
r - радиус окружности (в данном случае 1, так как это единичная окружность)
θ - угол в радианах (в данном случае π/3)
Подставляя значения в формулы, получаем:
x = 1 * cos(π/3)
y = 1 * sin(π/3)
Теперь нужно найти значения функций cos(π/3) и sin(π/3).
Значение cos(π/3) можно найти, зная, что тригонометрическая функция косинуса определяется как отношение прилежащего катета к гипотенузе прямоугольного треугольника, где угол π/3 соответствует одному из углов равностороннего треугольника (катет равен 1, гипотенуза равна 2). Таким образом,
cos(π/3) = 1/2
Значение sin(π/3) можно найти по аналогии, с помощью отношения противоположного катета к гипотенузе равностороннего треугольника.
sin(π/3) = √3/2
Теперь, подставляя значения функций в формулы, получаем искомые координаты:
x = 1 * cos(π/3) = 1/2
y = 1 * sin(π/3) = √3/2
Таким образом, координаты точки P(π/3) на числовой окружности равны (1/2, √3/2).
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Популярные вопросы
- Корнеплоды моркови выполняют функцию?...
1 - Перепиши следующие предложения,заменяя выделенные слова на she.he.they.it.we....
1 - Из двух дробей 6,156 и 6,1095 какая меньше?...
3 - Сумма 3-х чисел равна 480 1-ое число состовляет 30%от всего 2-ое 55% от всего.найдите...
1 - Вычеслить ! 400м-50см 5км650м+17км 8км670м-938м 200км-25км80см...
3 - Фразеологизма душа в пятки ушла ! зарание...
1 - Какое предложение можно составить из слов хлопок хлопок...
3 - Сочинение по картине васнецова богатыри...
3 - 248 кг + 3 ц 600 см кв - 4 дм кв 5 см кв сколько будет...
2 - Вводу массой m1=1 кг , температура которой t1=10 градусов , вливают кипяток...
2