Определение квадратного уравнения: Квадратное уравнение-это уравнение вида ax^2+bx+c=0, где коэффициенты a, b и c-произвольные числа, причем "а" не равен нулю.
И вот теперь мои вопросы:
1)Как понять: "уравнение вида...". Что это значит? Какого вида?
2)Я знаю что коэффициенты-это числовые или буквенные множители, но что значат числовые или буквенные множители? Что это вообще за множители и что такое множители? Ещё я знаю что коэффициенты-это число, стоящее перед буквой. Например: 5с=5, 8f=8, х=1.
3)И ещё, почему "а" не равен нулю? Как это объяснить простыми словами?
, объясните всё простыми словами, чтоб не создавать ещё больше вопросов. Заранее всем !
Другие вопросы по теме Алгебра
Популярные вопросы
- Проанализировать стихотворение Е.Евтушенко « о пианисте»,...
3 - Зависимость задали следующим образом: каждому целому числу поставили в соответствие...
1 - с физикой Работа электрического поля по перемещению зарядов. Вычислим работу...
2 - нужно написать короткое сообщение или статью в газету по теме Будущее Казахстана:Глазами...
1 - К раствору бромоводорода добавили 6г гидроксида натрия. Рассчитайте массу бромида...
2 - Как по вашему относились к Абаю его современники? ...
3 - Кто из названных правителей был участником Крестовых походов?...
3 - Який час children started doing something...
1 - 88.Сосатвьте из слов первой и второй группы пары синонимов и запишите их. Какие...
3 - Напишите уравнения диссоциации электролитов:HNO3,FeCl3,NaOH...
2
***
1)
уравнение вида "ax² + bx +c = 0"
например 2x² + 6x + 10= 0
а = 2, b = 6, c = 10
3)
если а будет равен нулю тогда умножив ее на х² получится 0 тогда
уравнение больше не будет квадратным,
поэтому
а≠0
2)
множитель это любое число, которое показывает сколько раз умножить другое число, которое называют множимым
множимое это число, которое умножают,
а множитель это число на которое умножают.
допустим 9 х 4,
9 - множимое
4 - множитель
числа называют числовыми множителями одночлена, а буквы буквенными множителями одночлена
например:
7abc
7 - числовой множитель
a, b, c - буквенные множители
коэффициент _ числовой множитель при буквенном выражении
например:
в "7х" ,
коэффициент 7, (при переменной x)
в 20х
коэффициент 20, (при переменной x)
ответ.
Квадратное уравнение-это уравнение вида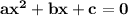 , где коэффициенты
, где коэффициенты 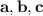 - произвольные числа причём
- произвольные числа причём 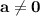 .
.
Такую запись квадратного уравнения часто называют записью в общем виде .
1) Как понять: "уравнение вида..." . Очень просто . Это значит, что если ты видишь уравнение, похожее по записи на написанное выше , то перед тобой квадратное уравнение . Единственное отличие будет в том, что вместо букв a, b, c будут стоять конкретные числа .
Надо помнить, что если какое-либо из чисел a, b, c равно 1 , то это число можно не писать в качестве множителя .
И ещё надо помнить, что умножение на число 0 даёт 0 . Поэтому , если какое-либо из чисел a, b, c равно 0, то такой член с нулевым множителем вообще будет отсутствовать .
Например,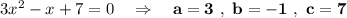 ,
,
3) Если же именно число а=0 , то мы получим такую запись :
Уже понятно, что мы в такой записи уравнения не видим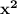 . А значит уравнение не будет квадратным .
. А значит уравнение не будет квадратным .
Вывод. Если хочешь иметь квадратное уравнение обязательно в этом уравнении должен присутствовать член с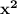 , остальные члены уравнения могут и не присутствовать ( тогда
, остальные члены уравнения могут и не присутствовать ( тогда 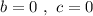 ) .
) .
То есть обязательно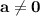 .
.
2) Числа , которые умножают друг на друга, называют множителями . Множители бывают числовые и буквенные .
Например,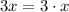 . Первый множитель равен числу 3, а второй множитель - это буква х .
. Первый множитель равен числу 3, а второй множитель - это буква х .
В уравнениях, где присутствует переменная х , обычно числовые множители называют коэффициентами и их обозначают в общем виде буквами латинского алфавита . В записи квадратного уравнения - это коэффициенты a, b и c . В предыдущем примере коэффициентом является число 3 .
Так, в квадратном уравнении числовой множитель перед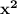 , который мы в общей записи обозначили буквой а , называют старшим коэффициентом , числовой множитель перед х называют вторым коэффициентом -это b , а число с называют свободным членом (он свободен от умножения на х ) .
, который мы в общей записи обозначили буквой а , называют старшим коэффициентом , числовой множитель перед х называют вторым коэффициентом -это b , а число с называют свободным членом (он свободен от умножения на х ) .