Опишите алгебраически прямоугольник, симметричный относительно оси абцисс прямоугольнику, заданому условиями: 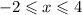
И
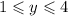
Другие вопросы по теме Алгебра
Популярные вопросы
- Исследуйте функцию с производной и постройте её график...
2 - • Ойынды дәлелдеу үшін керек сөз тіркесін таңда. талантты болу керек жаттығу...
2 - Как это делать разобраться! кто понимает химию!?)...
2 - Решить по условию не смотря на решение...
3 - 5 Complete the sentences with the correct prepositions. Use your dictionary...
3 - Определите структуру ассортимента в натуральном и денежном выражении...
1 - F 4. Расстояние от А до D равно 8 см. Чему равно расстояние от С до В? Почему?...
2 - Решите неравенство 3x2-11x-4 0...
3 - У зошиті заповніть таблицю (ФГП південної Америки?...
1 - 1 1. Програма переводу вихідного коду в двійковий називається...
1
Дан прямоугольник, границы которого заданы в условии неравенствами:
-2 ≤ x ≤ 4 и 1 ≤ y ≤ 4.
Мы хотим найти алгебраическое уравнение прямоугольника, симметричного относительно оси абсцисс (горизонтальной оси), которое бы задавало этот прямоугольник.
Поскольку прямоугольник симметричен относительно оси абсцисс, его верхняя и нижняя границы должны быть равны в абсолютной величине, но противоположны по знаку.
В данном случае, y координаты верхней и нижней границы прямоугольника равны по модулю, но имеют разный знак. Верхняя граница - 4, а нижняя - (-1); положительное и отрицательное направление относительно оси абсцисс.
Таким образом, можно выразить алгебраическое уравнение прямоугольника симметричного относительно оси абсцисс следующим образом:
y = -|x| + 5
Теперь можно привести пошаговое решение для объяснения школьнику:
Шаг 1: Рассмотрим нижнюю границу прямоугольника. Она задана неравенством -2 ≤ x ≤ 4. Чтобы выразить эту нижнюю границу в алгебраической форме, используем выражение x = -2.
Шаг 2: Рассмотрим верхнюю границу прямоугольника. Она задана неравенством 1 ≤ y ≤ 4. Заменим y на -|x| + 5, где x - это нижняя граница.
Шаг 3: Получаем уравнение прямоугольника: y = -|x| + 5, где -2 ≤ x ≤ 4.
Теперь, если мы подставим значения x из интервала -2 ≤ x ≤ 4 в это уравнение, мы получим различные значения y, которые находятся в заданном интервале 1 ≤ y ≤ 4.
Например, при x = -2, получаем y = -|-2| + 5 = -2 + 5 = 3, что соответствует заданным условиям. То же самое будет при других значениях x из интервала -2 ≤ x ≤ 4.
Таким образом, уравнение y = -|x| + 5 задает алгебраически прямоугольник, симметричный относительно оси абсцисс, с границами -2 ≤ x ≤ 4 и 1 ≤ y ≤ 4.