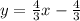Окружность задана уравнением (x-1)^2+y^2= 9 напишите уравнение прямой проходящей через ее центр и точку а(3,4)
Другие вопросы по теме Алгебра
Популярные вопросы
- Составьте 8 вопросов с ответами к кроссворду на тему три толстяка...
2 - Байга.реши пример и обгони соперника.а)20-9+4 б) 12+3-4...
3 - Какой из организмов является одноклеточным? дрожжи гидра ряска дождевой...
3 - Всегда ли хорошо быть идеально правильным человеком?...
1 - Составь преложения из словосочитания: чувствовать себя, представлять...
1 - Вдвух бочках одинаковое количество воды.когда из одной бочки взяли...
3 - Как северо-восточная русь , новгородская земля...
3 - 6класс. можете . можно записывать только ответы. 20. вычислите:...
2 - 1.найди неправильное уравнения! а.4267÷17,б.223×32,в.9947÷49,г.39×214,д.729÷27,...
1 - Отметить на предложение. девочки цветы и не стали их рвать?...
1
Уравнение прямой имеет вид y = kx + b.
По условию, центр окружности имеет координаты (1;0). Найдем уравнение прямой, проходящей через две заданные точки, подставив их координаты в уравнение прямой
Искомое уравнение прямой: