Около равностороннего конуса описан шар найти отношение поверхности шара к полной поверхности конуса

Question

Алгебра: Около равностороннего конуса описан шар найти отношение поверхности шара к полной поверхности конуса

cjhjrf1212 · Answer

Судя по всему, равносторонний конус - это Конус, осевой сечение которого является равносторонним треугольником.

Для сферы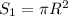 $S_1=\pi R^2$

Для полной поверхности конуса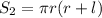 $S_2=\pi r(r+l)$

Чертеж к задаче во вложении.

Рассмотрим осевое сечение описанного конуса. Получим равносторонний треугольник АВС, вокруг которого описана окружность. с центром в точке О.

Для правильного треугольника АВС AC=l=2r и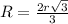 $R=\frac{2r\sqrt3}{3}$

Составим отношение площадей поверхностей:

$\frac{S_1}{S_2}=\frac{4\pi R^2}{\pi r(r+l)}=\frac{4(\frac{2r\sqrt3}{3})^2}{r(r+2r)}=\frac{16}{9}$

ответ : 16:9