. Очень нужно. 36.11. Найдите предел:
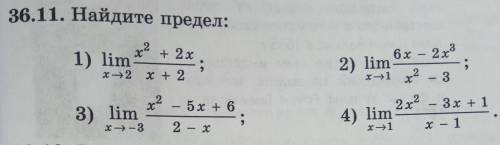
Другие вопросы по теме Алгебра
Популярные вопросы
- Ех. 4 explain the use of the present continuous in the following sentences и...
3 - Почему роман робинзон крузо называется романом воспитания? !...
1 - Напишите сочинение рассуждение на тему какие произведения а.с. пушкина мне нравится...
2 - Среди бактерий жгутики могут иметь: 1)кокки 2)бациллы 3)вибрионы 4)спириллы...
1 - Самый первый алфавит создан 1)сыма цянь 2)яссави 3)аль-фараби 4)кашгари...
2 - Вини-пух заготовил на зиму 97 горшков мёда. за январь он сьел 36 горшков, после...
2 - Славяне называли ноябрь грудень, листогной, полузимник. объясните народные названия...
3 - 268 девушек из 172 стран мира уже прислали свои заявки на участие в международном...
3 - На 15 га пашни было посеяно 24 ц зерна.сколько зерна потребуется,чтобы засеять...
2 - Цена стиральной машины снижена на 20% и теперь она стоит 310 евро.сколько стоила...
1
Исходное выражение: (5x^2 + 3x - 1) / (x^2 + 2x + 1)
1. Раскроем скобки в числителе и заменим (5x^2 + 3x - 1) на 5x^2 + 3x - 1:
(5x^2 + 3x - 1) / (x^2 + 2x + 1)
2. Упростим выражение:
5x^2 + 3x - 1 / x^2 + 2x + 1
3. Применим правило нахождения предела для рациональной функции:
Предел рациональной функции находим, вынося общий множитель из числителя и знаменателя.
В нашем случае общим множителем является x^2, поэтому выносим его:
x^2(5 + 3/x - 1/x^2) / x^2(1 + 2/x + 1/x^2)
4. Упростим полученное выражение:
(5 + 3/x - 1/x^2) / (1 + 2/x + 1/x^2)
5. Теперь найдем пределы отдельно для числителя и знаменателя:
a) Найдем предел числителя:
lim(x->∞) (5 + 3/x - 1/x^2) = 5 + 0 - 0 = 5
b) Найдем предел знаменателя:
lim(x->∞) (1 + 2/x + 1/x^2) = 1 + 0 + 0 = 1
6. Теперь найдем предел всего выражения, подставив найденные пределы для числителя и знаменателя:
lim(x->∞) ((5 + 3/x - 1/x^2) / (1 + 2/x + 1/x^2)) = 5/1 = 5
Таким образом, предел данной функции при x стремящемся к бесконечности равен 5.