Объясните подробно, тему числовые неравенства и как строить рисункии т.п. я в 8 классе.

Нера́венство — одно из фундаментальных понятий математики.

Если два вещественных числа a и b соединены знаком неравенства или одним из отношений порядка , или , или , или же , установленных между числами, то говорят, что задано числовое неравенство.

Неравенства отношений , называют строгими, неравенства , называют нестрогими.

Неравенства отношений и , а также неравенства и называются неравенствами одного знака (одного смысла), неравества и , а также и ,< и , и называются неравенствами разного смысла (разного знака)

Окей. Записываю все свойства.

1. Если a>b, то b<а. Верное и обратное.

2. Если a>b и b>c, то a>c. Верное и обратное.

3. Если a>b, то для любого c a+c>b+c. Верно и обратное.

4. Если a>b, то для любого c>0 ac>bc. Верно и обратное.

5. Если a>b, то для любого c<0 ac<bc. Верно и обратное.

6. Если a>b и c>d, то a+c>b+d.

7. Если a>b и c<d, то a-c<b-d.

8. Если a>b, b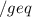  0 и , то 

9. Если  и  ,то 

10. Если , то для любого натурального  справедливо