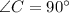Обьясните кто нибудь что такое арк косинус,синус,катангенс и тангенс или хотя бы 2 последних, мне не понять нечего

Сама приставка АРК, к любой функции, обозночает ее обратность.

Для наилементарнейшего понятия: 

Например arccos

arccosA=a; cosa=A; a[0;П]; A[-1;1]

Если длинное понятие, то Аркосинус числа А называеться число косинус которого равен а и который принадлежит промежутку от [0;п]

sin (синус) - отношение противолежащего катета к гипотенузе

cos (косинус) - отношение прилежащего катета к гипотенузе

tg (тангенс) - отношение противолежащего катета к прилежащему

ctg (котангенс) - отношение прилежащего катета к противолежащему

arcsin (арксинус) - арксинусом числа х есть значение угла А, для которого sinA=x

arccos (арккосинус) - арккосинусом числа х есть значение угла А, для которого cosA=x

arctg (арктангенс) - арктангенсом числа х есть значение угла А, для которого tgA=x

arcctg (арккотангенс) - арккотангенсом числа х есть значение угла А, для которого ctgA=x

Из  ABC