Обчисліть площу бічної поверхні піраміди Хеопса. Відомо, що вона має форму правильної чотирикутної піраміди. Сторона основи дорівнює 232 метри, а висота піраміди 147 метрів.
Другие вопросы по теме Алгебра
Популярные вопросы
- Почему игру, учение, труд называют ведущими деятельность? ! до завтра...
2 - Написать небольшой рассказ на тему берегите природу там должны быть числительные...
1 - Социальные нормы меня и моей семьи? ! ...
2 - Текст по ійській твій найкращій навчальний день. за критеріями в книжкі...
1 - Площа бічної поверхні правильної чотирикутної призми дорівнює 96 см^2...
1 - Вшколе города n-ска некоторые ученики знают только , некоторые только...
1 - 1) выполните деление с остатком на число 7 следующих чисел: 0, 15, 253,...
3 - По украинской визначте сюжеті елементи повісті,, дорогою ціною...
2 - Для разветвленной цем постоянного тока с несколькими источниками энергии...
3 - Қастек баянбаев деген кім? -ол қандай ақындарымыздың бірі? -оның ға арналған...
2
ответ: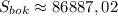 м² .
м² .