НУЖНО ВСЕ ЗАДАНИЕ. НО НУЖНО ПОДРОБНО, ЧТОБ Я ПОНЯЛА .еСЛИ НЕ ЗНАЕТЕ ВСЕ,ТО ВЫПОЛНИТЕ ТЕ НОМЕРА КОТОРЫЕ МОЖИТЕ.

НУЖНО ВСЕ ЗАДАНИЕ. НО НУЖНО ПОДРОБНО, ЧТОБ Я ПОНЯЛА .еСЛИ НЕ ЗНАЕТЕ ВСЕ,ТО ВЫПОЛНИТЕ ТЕ НОМЕРА КОТОР

Ответы

Arse12345 15.10.2020 17:41

1) у=5х-2 прямая. Ей параллельна прямая, у которой такой же угловой коэффициент, то есть k=5 . Это прямые б) у=5х и г) у=5х-6 .

2) у=0,5х-3

На оси ОУ выполняется соотношение: х=0 ⇒ у(0)= -3 ⇒

Точка пересечения прямой с ОУ - это точка (0,-3) . ответ: в) .

3) у= -0,5х+1

Подставим координаты заданных точек в уравнение прямой. Если получим верное равенство, то точка лежит на этой прямой. Если равенства неверные, то точка не лежит на прямой .

А(-1,0): 0= -0,5*(-1)+1 , 0=0,5+1 , 0=1,5 неверно ⇒ точка не лежит на прямой

В(-2: 2,5): -2= -0,5*2,5+1 ⇒ -2= -0,25 неверно , не лежит

С(-2,0): 0= -0,5*(-2)+1 , 0=1+1 , 0=2 неверно , не лежит

D(0,1): 1= -0,5*0+1 , 1=1 верно ⇒ точка лежит на прямой

ответ: г) .

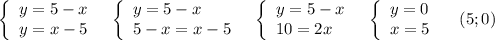
4) $\left\{\begin{array}{ccc}y=5-x\\y=x-5\end{array}\right\ \ \left\{\begin{array}{l}y=5-x\\5-x=x-5\end{array}\right\ \ \left\{\begin{array}{l}y=5-x\\10=2x\end{array}\right\ \ \left\{\begin{array}{l}y=0\\x=5\end{array}\right\ \ \ (5;0)$

ответ: г) .

5) Верный ответ б) : k>0 , b<0 .

k>0 ⇒ прямая образует острый угол с положительным направлением оси ОХ ,

b<0 ⇒ прямая пересекает ось ОУ ниже оси ОХ ( точка пересечения имеет отрицательную ординату) .

ПОКАЗАТЬ ОТВЕТЫ

TinoShtrydenberg 15.10.2020 17:41

1) б, в, г.

2) в.

3) г.

4) г.

5) б.

Объяснение:

1) Вид прямолинейной функций: Y=KX+B, где К-это угловой коэффициент при Х, а В-это величина смещения прямой относительно центра координат. Графики прямолинейных функций параллельны в том случае, когда угловые коэффициенты К и знак перед К при х совпадают, но при этом различные B. По существу К-это угол наклона между графиком прямой и осью Х. Если угол наклона одинаков, то прямые параллельны.

2) Для нахождения точки пересечения оси Y, нужно X прировнять к 0, и подставить в выражение функций: y=-0,5*0+1=1. Искомая точка (0;1).

3) Если точка принадлежит графику функций, то при подстановке координаты точки Х в выражение функций, значение функций должно совпасть со значением Y координаты точки.

Пример 1: т. D(0;1), у(0)=-0,5*0+1=1, значение функций совпало со значением координаты Y точки D. Следовательно точка D принадлежит графику функций.

Пример 2: т. А(-1;0), у(-1)=-0,5*(-1)+1=1,5, значение функций не совпадает со значением координаты Y точки A. Следовательно точка А не принадлежит графику функций.

4) Чтобы найти точки пересечения двух графиков функций, нужно составить из них систему уравнений. Корни системы уравнений и будут точки пересечения графиков функций. Составим систему:

$\left \{ {{y=5-x} \atop {y=x-5}} \right.$

5-x=x-5

-2*x=-10

x=5 - это координата Х точки пересечения. Найдём координату Y подставив х=5 в любое из уравнений:

у=5-х=5-5=0 - это координата Y точки пересечения. Точка пересечения c координатами: (5;0).

5) Если B<0, то график прямолинейной функций ниже начала координат. Если B>0, то график прямолинейной функций выше начала координат. В данном случае он ниже начала координат.

Если К>0, то график расположен в первой и третьей четверти координатной плоскости. Если К<0, то график расположен во второй и четвёртой четверти координатной плоскости.