. Нужно решить уравнение (3), логарифмируя обе его части
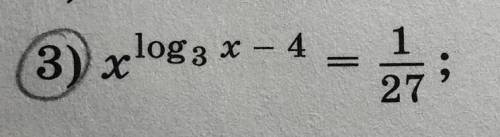
Другие вопросы по теме Алгебра
Популярные вопросы
- Діалог на тему плюси та мінуси дистанційного навчання...
3 - Определите правильно пиломатериалы...
1 - Закончите предложения подходящими по смыслу предлогами. ( for, of, in, to, across,...
3 - Розв яжіть благаю ів.Благаюююююю...
3 - Пояс горных джайлау по природным и экономическим условиям делятся на части А)альпийские...
2 - и кто ответит правильно тому отмечаю как самый лучший...
2 - Найдите корни, подберите однокоренные слова: ощипать, грошовый, увязать, обнажить,...
2 - Задание 3. Вклад казахских ханов в становление и развитие законодательной системы...
2 - Середнє арифматичне чисел 9,2 і У дорівнюєь 13,46. Знайдіть число У...
2 - Списать текст, вставляя пропущенные буквы и необходимые знаки препинания Гроза...
3
Объяснение: