нужно решить логарифмические уравнения
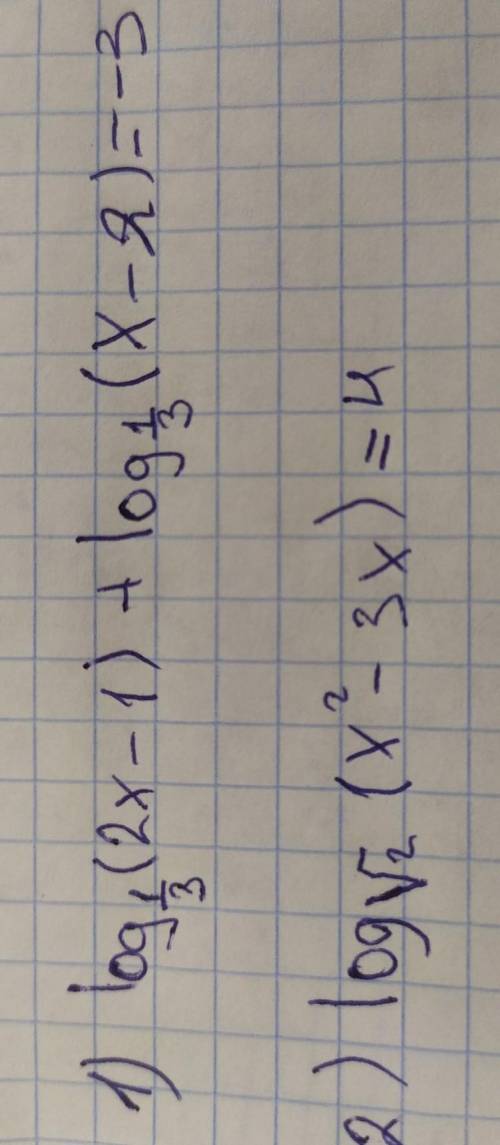
Другие вопросы по теме Алгебра
Популярные вопросы
- Характеристика Ассоль и Грея...
1 - Pr. Simple Утвердительное предложение: подлежащее глагол с окончанием s (3л, ед.ч)...
1 - Твір роздум Чому важливе дотримання взаємних прав і обов язків батьків та дітей...
2 - 1. Что означает запись 40, 50,...
1 - Которые «спрятались».5. Приведи примеры упругой и пластической деформации,...
1 - Знайти область визначення функції ...
2 - Письмово пояснити в зошиті зміст обраних хайку Хайку літо в Японії,цвітіння сакури...
2 - краткое описание про ивашку кудряшкина из расказа горячий камень А. Гайдар...
1 - Назвіть якості та риси характеру, які на ваш погляд роблять людей привабливими,...
3 - Розкрити дужки у виразі -5р(-х+2у-3к)...
1
1.
ОДЗ:
корень -1 не подходит.
ответ: 3.5
ОДЗ:
ответ: -1; 4.