нужно решить 5 примеров по алгебре
типа упростить, примерно так:
х²-5х+6
х²-5х+6=(х²-2х*5/2+25/4)-25/4+6=(х-5/2)²-1/4
(х-5/2)²-1/4=0
(х-5/2)²=1/4
х-5/2=1/2 х-5/2=-1/2
х=3 х=-2

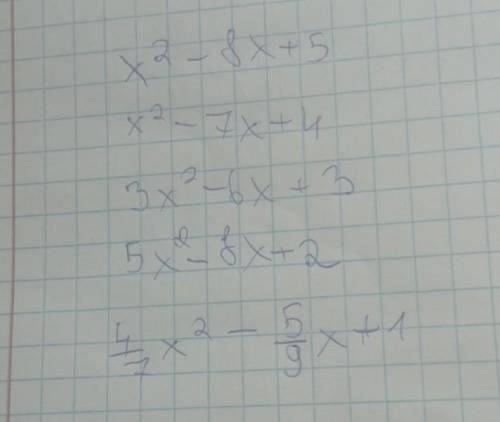
нужно решить 5 примеров по алгебретипа упростить, примерно так:х²-5х+6х²-5х+6=(х²-2х*5/2+25/4)-25/4+

Ответы

katuwka20032003 14.02.2022 06:01

вам надо выделить полный квадрат, а потом решить уравнение.

1. х²-8х+5=(х²-2*х*4+16)-16+5=(х-4)²-11; (х-4)²-11=0; (х-4)²=11; (х-4)=±√11; х=4+√11;х=4-√11

2. х²-7х+4=(х²-2*х*3.5+12.25)-12.25+4=(х-3.5)²-8.25; (х-3.5)²-8.25=0; (х-3.5)²=8.25; (х-3.5)=±√8.25; х=3.5±√8.25; х=3.5+√8.25; х=(7+√33)/2;

х=(7-√33)/2;

3. 3*(х²-2х+1)=3*(х-1)²; 3*(х-1)²=0; 3≠0; х-1=0; х=1

4. 5х²-8х+2=5*(х²-8х/5+2/5)=5((х²-2*х*4/5+16/25)-16/25+10/25)=

5((х-/5)²-6/25); 5((х-4/5)²-6/25)=0; (х-4/5)²-6/25=0; х-4/5=±√6/5; х=(4+√6)/5;

х=(4-√6)/5;

5. 4х²/7-5х/9+1=(4/7)*(х²-35х/36+7/4)=

(4/7)*((х²-2*х*35/72+1225/5184)-1225/51847/4+7/4)=

(4/7)*((х-35/72)²-1225/5184+7/4)=

(4/7)*((х-35/72)²+(-1225+9072)/5184)=(4/7)*((х-35/72)²+7847/5184) это выражение нулю не равно, т.к. это сумма неотрицательного и положительного чисел. тут корней нету уравнения 4х²/7-5х/9+1=0

ПОКАЗАТЬ ОТВЕТЫ

keti261 14.02.2022 06:01

Выделяем полные квадраты, используя формулу квадрата разности

a^2-2ab+b^3=(a-b)^2 .

$1)\ \ x^2-8x+5=(x^2-2\cdot 4x+16)-16+5=(x-4)^2-11(x-4)^2-11=0\ \ ,\qquad \boxed{\ a^2-b^2=(a-b)(a+b)\ }Big((x-4)-\sqrt{11}\Big)\Big((x-4)+\sqrt{11}\Big)=0a)\ \ x-4-\sqrt{11}=0\ \ ,\ \ x_1=4+\sqrt{11}b)\ \ x-4+\sqrt{11}=0\ \ ,\ \ x_2=4-\sqrt{11}Otvet:\ x_1=4+\sqrt{11}\ ,\ x_2=4-\sqrt{11}\ .$

$2)\ \ x^2-7x+4=(x^2-2\cdot \dfrac{7}{2}\, x+\dfrac{49}{4})-\dfrac{49}{4}+4=\Big(x-\dfrac{7}{2}\Big)^2-\dfrac{33}{4}Big(x-\dfrac{7}{2}\Big)^2-\dfrac{33}{4}=0\ \ ,\ \ \ \Big(x-\dfrac{7}{2}-\dfrac{\sqrt{33}}{2}\Big)\Big(x-\dfrac{7}{2}+\dfrac{\sqrt{33}}{2}\Big)=0a)\ \ x-\dfrac{7}{2}=\dfrac{\sqrt{33}}{2}\ \ ,\ \ x_1=\dfrac{7}{2}+\dfrac{\sqrt{33}}{2}b)\ \ x-\dfrac{7}{2}=-\dfrac{\sqrt{33}}{2}\ \ ,\ \ x_2=\dfrac{7}{2}-\dfrac{\sqrt{33}}{2}$

$Otvet:\ x_1=\dfrac{7}{2}+\dfrac{\sqrt{33}}{2}\ ,\ x_2=\dfrac{7}{2}-\dfrac{\sqrt{33}}{2}\ .$

$3)\ \ 3x^2-6x+3=3\, (x^2-2x+1)=3\, (x-1)^2(x-1)^2=0\ \ \Rightarrow \ \ \ x-1=0\ \ x=1Otvet:\ x=1\ .$

$4)\ \ 5x^2-8x+2=5\Big(x^2-\dfrac{8}{5}\, x\Big)+2=5\Big (x^2-2\cdot \dfrac{4}{5}\, x+\dfrac{16}{25}-\dfrac{16}{25}\Big)+2==5\, \Big(x-\dfrac{4}{5}\Big)^2-\dfrac{16}{5}+2=5\Big(x-\dfrac{4}{5}\Big)^2-\dfrac{6}{5}\ \ ,\ \ \ 5\Big(x-\dfrac{4}{5}\Big)^2-\dfrac{6}{5}=0\ ,Big(x-\dfrac{4}{5}\Big)^2-\dfrac{6}{25}=0\ \ \Rightarrow \ \ \Big(x-\dfrac{4}{5}-\dfrac{\sqrt{6}}{5}\Big)\Big(x-\dfrac{4}{5}+\dfrac{\sqrt{6}}{5}\Big)=0$

$x_1=\dfrac{4}{5}+\dfrac{\sqrt{6}}{5}\ \ ,\ \ \ x_2=\dfrac{4}{5}-\dfrac{\sqrt{6}}{5}\ \ - otvet$

$5)\ \ \dfrac{4}{7}x^2-\dfrac{5}{9}x+1=\dfrac{4}{7}\Big(x^2-\dfrac{35}{36}\, x\Big)+1=\dfrac{4}{7}\Big (x-2\cdot \dfrac{35}{72}\, x+\dfrac{35^2}{72^2}-\dfrac{35^2}{72^2}\Big)+1==\dfrac{4}{7}\, \Big(x-\dfrac{35}{72}\Big)^2-\dfrac{4\cdot 1225}{7\cdot 5184}+1=\underbrace{\dfrac{4}{7}\Big(x-\dfrac{35}{72}\Big)^2}_{\geq 0}+\underbrace{\dfrac{31388}{36288}}_{0}\, 0$