нужно решение хотябы пеоловины
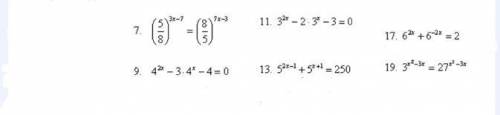
Другие вопросы по теме Алгебра
Популярные вопросы
- Найдите значение выражения, если tga=2:...
3 - Можете как-то схему мне прислать? можно в любой соцсети!...
3 - 3-тапсырма. Төмендегі тіркестерді пайдаланып сөйлем құрастырыңыз. Күні...
1 - Зробіть морфологічний розбір слів казок бузок...
3 - ів хто виконає ці два завдання...
3 - 24:15 = 8:5 проверить пропорцию, выделете крайние члены...
2 - Составить сравнительную таблицу §5 Первые правители Древнерусского государства.В...
2 - Яких значень набудуть змінні j та i після обчислення для int j, i =...
3 - Рівняння реакції магній з натрій хлоридом...
3 - Опишите свойства живых организмов: дыхание, питание, рост, развитие,...
2
замена:
нет корней
ответ: 1.
замена:
нет корней
ответ: 1.
замена: